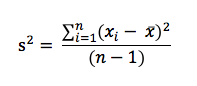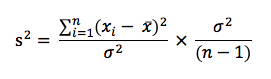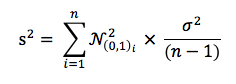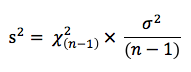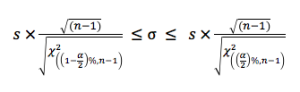Quelques considérations importantes concernant l’estimation des écarts-types
L’évaluation des écarts-types par les méthodes de type A est une étape importante dans l’estimation des incertitudes de mesure. Souvent, le métrologue se pose la question du nombre de valeurs qu’il faut répéter pour que l’estimation qu’il obtient soit d’une qualité suffisante.
La question du nombre d’échantillons mérite par conséquent que nous nous y attardions un peu afin de la considérer dans un contexte général …
- Le biais d’écart-type
La formule de l’écart-type calculée sur un échantillon de n valeurs x1,…,xn, telle que nous la connaissons (C’est à dire s’=![]() , dit écart-type empirique), n’estime pas sans biais le « véritable » écart-type « σ » (dit écart-type théorique) de la population dont l’échantillon est issu, c’est à dire l’objet mathématique qui a les propriétés que nous avons tous appris (68% des valeurs dans ± 1.σ si la loi parente est normale) ) et ceci est d’autant plus vrai que l’estimation est obtenue avec peu de valeurs (ce qui est souvent le cas en métrologie). Les statisticiens disent avec quelques raccourcis que l’écart-type est un estimateur biaisé de la racine carré de la variance (par contre s’² estime sans biais σ²). Le but de ce post n’est pas de développer cet aspect de l’évaluation des écarts-types mais le métrologue doit garder ce point à l’esprit. Ceci dit, ce problème est rarement impactant dans les calculs car l’écart-type évalué par une méthode de type A avec peu d’échantillons est rarement utilisé seul. Il est combiné à d’autres écarts-types, via la somme des carrés, ce qui augmente le nombre de degrés de liberté (DDL) et réduit le biais … En revanche, s’il devait être utilisé seul pour donner un intervalle de confiance, il conviendrait d’être vigilant. Pour mémoire, vous trouverez ci-dessous la formule du biais :
, dit écart-type empirique), n’estime pas sans biais le « véritable » écart-type « σ » (dit écart-type théorique) de la population dont l’échantillon est issu, c’est à dire l’objet mathématique qui a les propriétés que nous avons tous appris (68% des valeurs dans ± 1.σ si la loi parente est normale) ) et ceci est d’autant plus vrai que l’estimation est obtenue avec peu de valeurs (ce qui est souvent le cas en métrologie). Les statisticiens disent avec quelques raccourcis que l’écart-type est un estimateur biaisé de la racine carré de la variance (par contre s’² estime sans biais σ²). Le but de ce post n’est pas de développer cet aspect de l’évaluation des écarts-types mais le métrologue doit garder ce point à l’esprit. Ceci dit, ce problème est rarement impactant dans les calculs car l’écart-type évalué par une méthode de type A avec peu d’échantillons est rarement utilisé seul. Il est combiné à d’autres écarts-types, via la somme des carrés, ce qui augmente le nombre de degrés de liberté (DDL) et réduit le biais … En revanche, s’il devait être utilisé seul pour donner un intervalle de confiance, il conviendrait d’être vigilant. Pour mémoire, vous trouverez ci-dessous la formule du biais :
gnx s’ estime sans biais σ avec gn =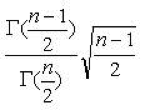
où Γ désigne la fonction Gamma d’Euler et n le nombre de valeurs disponibles.
| n |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| gn |
1,2533 |
1,1284 |
1,0854 |
1,0638 |
1,0509 |
1,0424 |
1,0362 |
1,0317 |
1,0281 |
1,0253 |
1,0230 |
1,0210 |
1,0194 |
1,0180 |
- L’intervalle de confiance d’un estimateur d’écart-type : description de la loi du Khi-deux
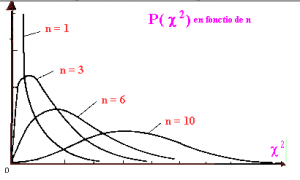
Tout comme la valeur vraie d’un mesurande ne pourra jamais être connue, la valeur de l’écart-type, notée généralement σ, ne sera elle non plus jamais connue. Le métrologue devra se contenter d’un estimateur de ce dernier, noté généralement s’ de ce dernier dont la qualité dépend du nombre d’échantillons qui aura servi à le calculer. Faute de connaitre la vraie valeur, les statisticiens ont étudié les propriétés de l’estimateur s’ de l’écart-type σ. Ils ont théorisé une loi de distribution qui a un grand intérêt dans l’estimation de l’intervalle de confiance de σ à partir de s’ et du nombre n de valeurs qui ont permis de le calculer. Il s’agit de la loi du Khi-Deux, notée généralement χ2 .
La loi du Khi-Deux est caractérisée par un nombre de degrés de liberté, c’est à dire le nombre de valeurs qui compose la somme qui la définit. En effet, la loi du Khi-Deux est une loi de probabilité qui représente la distribution des sommes obtenues à partir des carrés de n valeurs, lesdites n valeurs étant chacune des réalisations indépendantes d’une loi normale centrée réduite (Loi normale de moyenne 0 et d’écart-type 1). Cette somme est évidemment non seulement fonction du caractère aléatoire de chacune des valeurs qui la compose (d’où le fait qu’il s’agit d’une loi de probabilité) mais également du nombre n (nombre de degrés de liberté) de valeurs qui la compose.
La somme S est calculée suivant la formule :
Chaque terme de la somme étant des variables aléatoires, la somme elle-même devient une variable aléatoire et sa distribution est fonction du nombre n de degré de liberté.
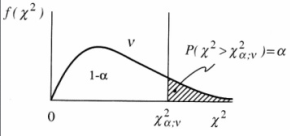
Lorsque cette loi de probabilité est connue, il n’est évidemment pas possible de deviner la somme qu’une expérience particulière produira. En revanche, il est possible de borner la valeur de ladite somme. En effet, on peut déterminer quelle est la probabilité pour que la somme S soit supérieure à une valeur limite ou inférieure à une autre, comme pour toutes les lois de probabilité. Les propriétés de la loi du Khi-deux permettent donc, en fonction du nombre de degrés de liberté, de donner un intervalle de confiance pour la somme qu’il est possible d’obtenir (dans la figure ci-dessous, le nombre de valeurs – DDL – est noté ν).
- Loi du Khi-Deux et encadrement d’un estimateur d’écart-type
Les propriétés de la loi du Khi-Deux permettent de donner un intervalle de confiance à un estimateur d’écart-type s’ et il est aisé de comprendre comment :
L’estimateur d’écart-type est donné par la formule suivante :
Pour faire apparaitre un Khi-Deux dans cette formule, il suffit de faire intervenir σ, inconnu, dans la formule précédente de la façon suivante :
Dans l’expression ci-dessus, le terme ![]() représente la somme de carrés de lois centrées réduites. En effet, en divisant la différence entre chaque xi et la moyenne de la série par l’écart-type de ladite série, on « normalise » la série. On transforme ainsi chaque variable aléatoire xi en une variable aléatoire de moyenne 0 et d’écart-type 1.
représente la somme de carrés de lois centrées réduites. En effet, en divisant la différence entre chaque xi et la moyenne de la série par l’écart-type de ladite série, on « normalise » la série. On transforme ainsi chaque variable aléatoire xi en une variable aléatoire de moyenne 0 et d’écart-type 1.
L’équation 1 ci-dessus peut-on se réécrire de la façon suivante :
ou encore :
La loi du Khi-Deux présente dans cette expression est effectivement une loi du Khi-Deux à (n-1) degrés de liberté car, pour normaliser la série, il a fallu calculer une moyenne, donc perdre un degré de liberté.
A partir de s’, calculé avec les valeurs expérimentales, et en utilisant les valeurs limites du Khi-Deux pour le niveau de confiance choisi (1-α), il est possible d’écrire l’inégalité suivante :
Le métrologue est souvent intéressé par la valeur maximale que peut prendre l’écart-type évalué, donc la borne supérieure de l’intervalle ci-dessus défini. En s’appuyant sur cette borne maximale, il est facile de répondre à la question du nombre de valeurs à recueillir pour calculer s. En effet, on peut commencer par 2 valeurs, calculer la borne et évaluer le poids de cette valeur maximale possible dans le bilan global d’incertitude. Si cette valeur reste négligeable dans le bilan global, on peut s’en tenir là et se limiter à 2 valeurs. Si, au contraire, elle n’est pas négligeable, on peut refaire 1, puis 2, puis 3 … puis n mesures jusqu’à ce que la valeur maximale se stabilise (on ne gagne plus beaucoup d’informations en ajoutant des mesures) ou devienne négligeable dans le bilan.
Plusieurs fonctions sont disponibles sur la dernière version d’Excel pour retourner les valeurs du Khi-Deux en fonction de la probabilité et du nombre de degrés de liberté. Les fonctions KHIDEUX.INVERSE(α;n) et LOI.KHIDEUX.INVERSE.DROITE(α;n) retournent toutes les deux la valeur du Khi-Deux au dessus de laquelle se trouve α% des valeurs (Zone hachurée de la figure « Valeur limite Khi-Deux » ci-dessus). La fonction LOI.KHIDEUX.INVERSE(α;n) retourne, quant à elle, qui couvre α% des valeurs possibles (Zone non hachurée de la figure « Valeur limite Khi-Deux » ci-dessus). Ainsi, LOI.KHIDEUX.INVERSE(α;n) = LOI.KHIDEUX.INVERSE.DROITE(1-α;n). Ce n’est pas simple, j’en conviens, mais c’est ainsi …
Le facteur qui permet de passer de s à sMax est donné par la formule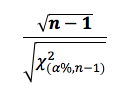 (suivant inégalité ci dessus) avec
(suivant inégalité ci dessus) avec ![]() comme la valeur retournée par la fonction LOI.KHIDEUX.INVERSE.(α;n-1) ou KHIDEUX.INVERSE (1-α;n-1) avec α = 5% si on souhaite déterminer la valeur maximale possible de σ à 95%.
comme la valeur retournée par la fonction LOI.KHIDEUX.INVERSE.(α;n-1) ou KHIDEUX.INVERSE (1-α;n-1) avec α = 5% si on souhaite déterminer la valeur maximale possible de σ à 95%.
Le graphe ci-dessous montre l’évolution de ce facteur en fonction du nombre n d’échantillons. On notera qu’à partir de 5 ou 6 valeurs, le facteur décroit très faiblement. On ne gagne par exemple que 10% sur la valeur du coefficient en passant de 15 à 30 valeurs …
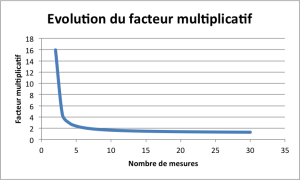
Toute cette théorie du Khi-Deux permet donc, à partir de quelques données, de déterminer un intervalle de confiance pour le σ recherché et d’adapter le nombre de mesures (d’échantillons) au contexte. Pas de règle d’or en effet pour le nombre d’observations …
Néanmoins, tout ce qui est écrit ci-dessus repose sur une hypothèse importante : la loi parente, c’est à dire la population de laquelle sont extraits les échantillons, suit une loi normale. Quand est-il si cela n’est pas le cas ?
- Cas des lois parentes Uniforme et Dérivée d’Arc-Sinus.
Pour contourner la difficulté théorique de réécrire toute la théorie du Khi-Deux pour des lois parentes différentes des lois centrées réduites, nous pouvons facilement utiliser la simulation numérique. En effet, il est relativement simple de simuler des lois uniformes centrées réduites ou des lois dérivées d’arc-sinus centrées réduites pour obtenir les sommes de n de leurs carrés et reproduire ainsi ce qui se passe pour le Khi-Deux. On peut ensuite retrouver « graphiquement » les valeurs limites dont nous avons besoin pour estimer, à partir de s’, le sMax possible, au niveau de confiance choisi.
-
- Cas d’une loi parente Uniforme
Dans le cas d’un échantillon de 4 valeurs, et pour obtenir le sMax à 90% de niveau de confiance, il faut multiplier s’ par Racine(4-1) / Racine (0,9736) = 1,755 alors que, dans une même configuration, une correction pour une loi parente normale aurait donné 2,2658. En faisant l’hypothèse classique que la population est normale (alors qu’elle est uniforme en réalité), le coefficient utilisé majore considérablement (près de 30%) la réalité. D’un point de vue « Risque », il n’est pas aberrant d’utiliser ce coefficient. Du point de vue « Coût », on peut, dans certains cas, se poser des questions …
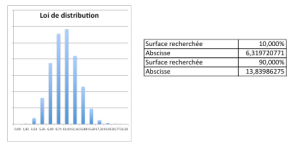
Dans le cas d’un échantillon de 11 valeurs, et pour obtenir le sMax à 90% de niveau de confiance, il faut multiplier s’ par Racine(11-1) / Racine (6,3197) = 1,2579 alors que, dans une même configuration, une correction pour une loi parente normale aurait donné 1,4337, soit près de 15% d’écart. Même conclusion que dans le cas précédent.
-
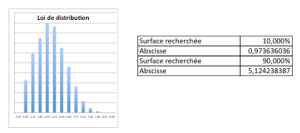
- Cas d’une loi parente Dérivée d’Arc-Sinus
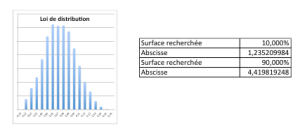
Distribution et valeurs limites pour un « Khi-Deux » à 3 DDL avec une loi parente en Dérivée d’Arc-Sinus
Dans le cas d’un échantillon de 4 valeurs, et pour obtenir le sMax à 90% de niveau de confiance, il faut multiplier s’ par Racine(4-1) / Racine (1,2352) = 1,5584 alors que, dans une même configuration, une correction pour une loi parente normale aurait donné 2,2658, soit plus de 45% d’écart !
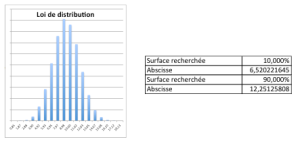
Distribution et valeurs limites pour un « Khi-Deux » à 10 DDL avec une loi parente en Dérivée d’Arc-Sinus
Dans le cas d’un échantillon de 11 valeurs, et pour obtenir le sMax à 90% de niveau de confiance, il faut multiplier s’ par Racine(11-1) / Racine (6,5202) = 1,2384 alors que, dans une même configuration, une correction pour une loi parente normale aurait donné 1,4337, soit plus de 15% d’écart.
Conclusion
La science statistique permet d’appréhender les phénomènes réels au travers de quelques échantillons. Néanmoins, et contrairement aux (mauvaises) habitudes que nous avons prises, il ne faut pas s’en tenir aux valeurs calculées. Il faut pousser le raisonnement et l’analyse pour pouvoir obtenir, à partir des données disponibles, des informations qui reflètent de façon satisfaisante la réalité recherchée.
Le métrologue doit acquérir cette compétence d’analyse. Elle est indispensable pour que les efforts consentis pour obtenir des données fiables conduisent à des décisions pertinentes…