2020
| Répétabilité : combien de mesures ? |  |
La question du nombre de mesures pour l’évaluation de la répétabilité est une question récurrente pour les métrologues. Je me souviens d’un temps déjà lointain où je m’interrogeais sur la formule qu’il convenait d’utiliser car on trouve beaucoup de choses sur ce sujet dans la littérature…
La science statistique nous offre pourtant des outils très simples pour répondre à cette question, que ce soit au moment de l’évaluation de cette répétabilité, par exemple dans le cadre d’un dossier d’accréditation, ou au cours des étalonnages car il n’est évidemment pas possible de répéter de nombreuses mesures en chaque point, pour des raisons évidentes de coût. Avant de découvrir ces outils, redisons quelques mots sur la notion essentielle d’estimateur, question au cœur du sujet …
Pourquoi parle-t-on d’estimateur ?
Tous les phénomènes aléatoires que nous rencontrons ne sont pas systématiquement de type gaussien. Il en existe de toute forme, certains pouvant être décrits par une loi mathématique (on parle alors de lois théoriques, par exemple la loi normale), d’autres par un histogramme (on parle alors de lois empiriques).
On connait bien la loi normale et ses propriétés car il est fréquent de croiser des phénomènes dont la loi de probabilité ressemble à cette loi théorique. Les statisticiens démontrent en effet que lorsque des phénomènes indépendants se mélangent, et sous réserves qu’aucun ne pèse plus de 30% de la variance totale, le phénomène résultant tend vers une loi normale. Quand tel est le cas, deux paramètres suffisent pour décrire la probabilité de réalisation de telle ou telle valeur possible du phénomène résultant : l’espérance mathématique (moyenne) et l’écart-type. Certaines lois de probabilité théoriques sont,quant à elles, décrites par plus de deux paramètres.
Si tout est simple en théorie, les choses se complexifient dans la pratique. En effet, connaitre la vraie espérance mathématique et le vrai écart-type d’une loi, normale ou non, supposent de disposer d’une infinité de réalisations du phénomène et cette infinité nous est évidemment inaccessible …
Si ces paramètres resteront inconnus dans le monde réel (et nous devons nous y faire !), il est toujours possible de simuler « un » monde réel et de se mettre à la place de l’expérimentateur pour observer ce qu’il est en mesure de « deviner » de la réalité grâce à ses observations.
Imaginons un phénomène gaussien, d’espérance mathématique égale à 0 et d’écart-type égal à 1. Imaginons également qu’un observateur dispose d’un grand nombre d’échantillons (2 000 dans cet exemple), tirés par simulation numérique et dont les effectifs varient de 2 à 50. Pour chaque échantillon, il est alors possible de calculer la moyenne (estimateur de l’espérance mathématique) et l’écart-type de chaque échantillon.
Note : Nous ne nous intéresserons, dans cet article, qu’à ce qui se passe sur les écarts-types, puisque nous nous intéressons à la répétabilité.
La figure ci-dessous donne des exemples de résultats numériques pour le calcul d’écarts-types sur des séries simulées et un graphe des résultats obtenus sur 2000 estimations.
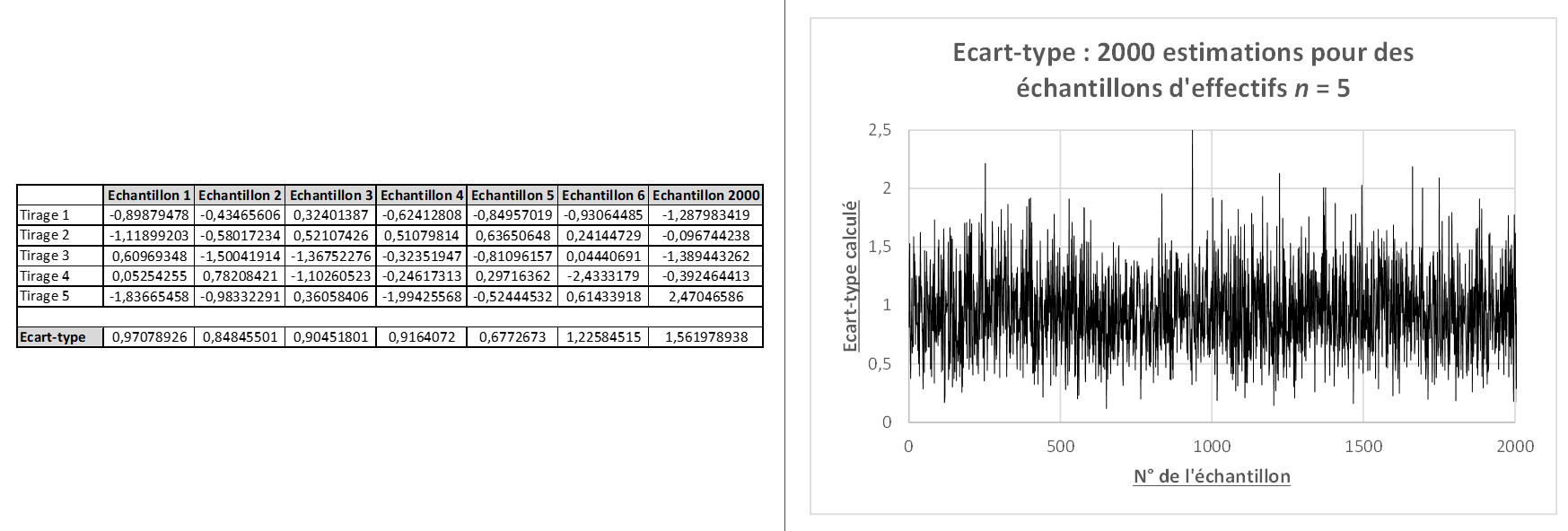
Figure 1 : Estimation d’écarts-types
Ces résultats mettent en évidence ce qu’exprime le concept « d’estimateur ». S’il était possible, pour chaque échantillon, de calculer le vrai écart-type, nous aurions obtenu, pour chacun des 2 000 échantillons, la même valeur égale à 1. Or, chaque échantillon, fruit du hasard de la simulation, conduit à des valeurs différentes pour l’écart-type, valeurs qui tournent bien sûr autour de la valeur vraie (qui vaut 1) mais qui ne sont pas systématiquement égales à 1. Il faut donc se résoudre à ne jamais disposer de l’écart-type vrai mais de devoir se contenter d’une estimation de cette valeur, estimation d’autant plus fiable que l’échantillon est de grande taille.
La Figure 2 ci-dessous est construite de la façon suivante. On calcule les 2 000 estimations de l’écart-type pour des échantillons d’effectifs variant de 2 à 50 puis on calcule les moyennes des 2 000 estimations d’écart-type pour chacun des effectifs. En traçant la moyenne des estimations d’écarts-types en fonction de l’effectif de l’échantillon (double trait), on constate clairement que ces moyennes sous-estiment la valeur vraie. En portant sur le même graphique un intervalle qui représente la dispersion des 2 000 estimations par effectif, on constate qu’elle diminue pendant que l’effectif augmente.
La courbe en pointillée rouge représente le ratio « R » entre la valeur vraie de l’écart-type (1) et la moyenne des estimations :
R = Valeur vraie / Valeur moyenne <=> Valeur Vraie = R x Valeur moyenne
C’est ce R qui caractérise le « biais de l’écart-type ». Les statisticiens démontrent que ce biais R est égal à :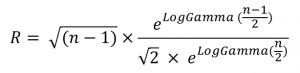
Le lecteur constatera la superposition quasi parfaite de la valeur expérimentale de R (Trait rouge en pointillé) et la valeur théorique (trait noir). On comprend ici, et ce sera utile plus bas, que si nous disposons d’un grand nombre d’échantillons d’effectif donné, le passage de la moyenne des écarts-types des échantillons à la valeur vraie de la population parente est possible, sous réserves que tous les échantillons proviennent d’une population d’écart-type constant…
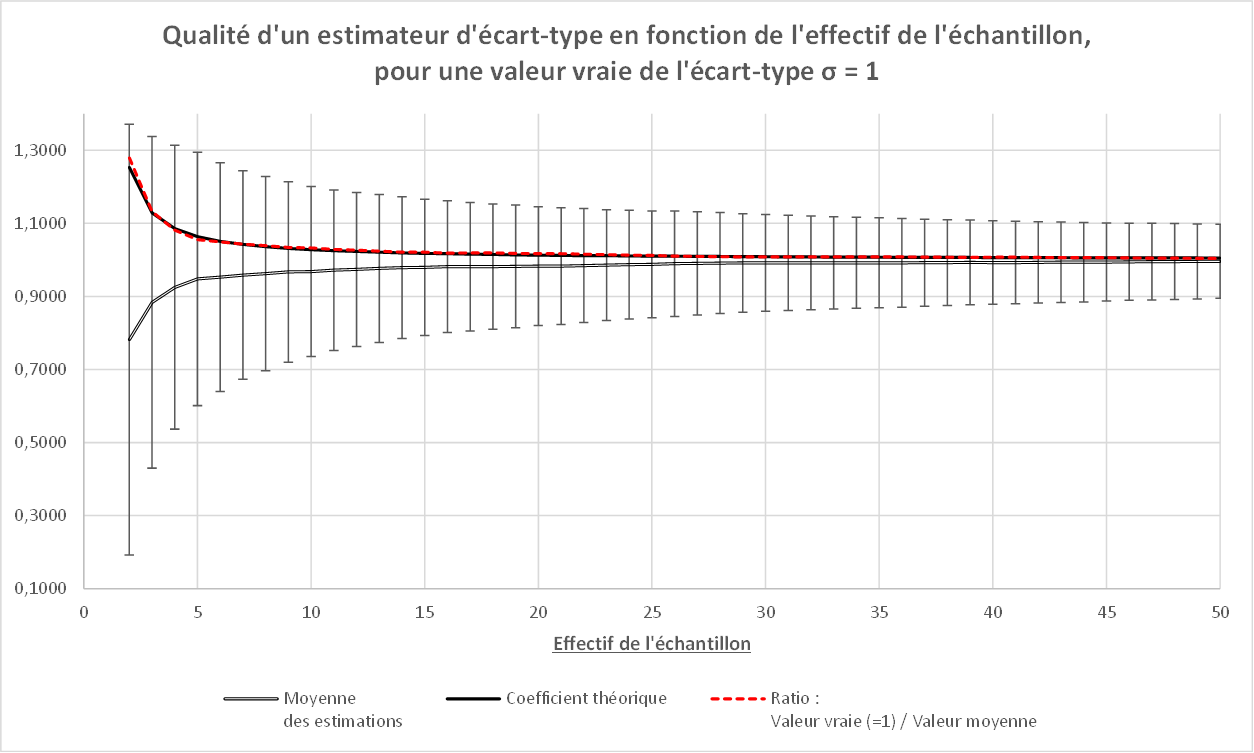
Figure 2 : Qualité de l’estimation d’un écart-type
La figure 2 permet également de répondre à la question du nombre de mesures qu’il faut faire pour évaluer de façon convenable l’écart-type de répétabilité. On remarque que le biais devient insignifiant au dessus de 25/30 valeurs (le lecteur pourra faire les calculs avec la formule de R). La dispersion (les barres d’incertitude), quant à elle, diminue rapidement au début puis le gain devient beaucoup moins important au delà de 25/30 mesures également. Voilà donc une bonne justification pour retenir le nombre de 25/30 mesures pour une évaluation pertinente (mais on verra ci-dessous qu’on peut faire beaucoup mieux, avec beaucoup moins …)
Petite note sur la variance …
Pour les mêmes données, on peut tracer la variance moyenne (carré de l’écart-type), plutôt que l’écart-type. On obtient alors la Figure 3 :
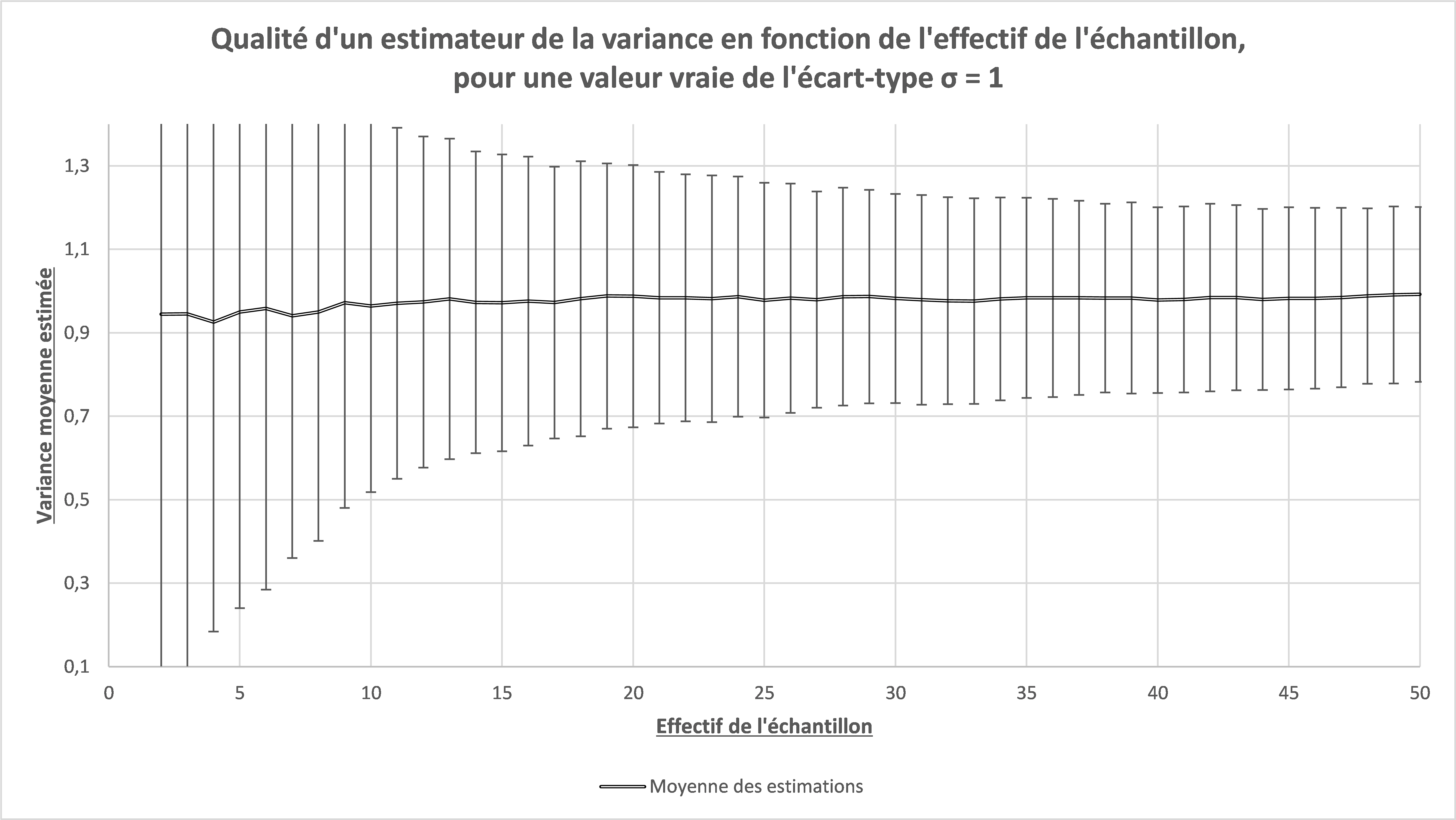
Figure 3 : Qualité de l’estimation d’une variance
On constate ici que, contrairement à l’écart-type, la variance est un estimateur non biaisée de la variance vraie (qui vaut 1 ici également : 12 = 1). Il est fondamental de comprendre cette propriété.
Dans un calcul d’incertitude, on additionne des variances, même si on estime, au départ, des écarts-types, que ce soit par une méthode de type A ou une méthode de type B. De ce fait, lors d’une évaluation de type A (notamment la répétabilité), et puisque nous savons que nous élèverons l’écart-type obtenu au carré pour avoir la variance, il ne faut surtout pas appliquer de correction pour le biais car cela entraînerait de facto une sur-évaluation possiblement conséquente de la variance !
25/30 mesures par point ? Impossible pour chaque étalonnage …
Le lecteur aura compris que 2, 3 voire 5 mesures ne permettront jamais de connaitre le vrai écart-type (Cf Figure 1). En revanche, les statisticiens ont mis au point la théorie des tests et ce sont ces tests qui peuvent nous permettre de trouver une solution acceptable au problème que pose la question des estimateurs.
Si le laboratoire peut (doit) consacrer de l’énergie pour évaluer proprement ses répétabilités, il ne peut évidemment pas recommencer à chaque étalonnage, et ce serait bien inutile. En fait, il suffit de tester si la série en cours, que son effectif soit égal à 2, 3 ou n, peut ou non provenir d’une population parente d’écart-type connu, c’est à dire l’écart-type de répétabilité étudié avec soin. Autrement dit, est-ce que la dispersion que j’observe sur le petit échantillon que représente mes mesures infirme, ou confirme, la répétabilité connue préalablement ?
Ce test est très simple à mettre en oeuvre. Il s’agit du test de Fisher Snédécor. Il suffit de calculer le ratio entre le carré de l’estimateur d’écart-type de l’échantillon et la variance de répétabilité (en portant le plus grand des deux au numérateur) et de comparer ce ratio à la valeur critique de Fisher :
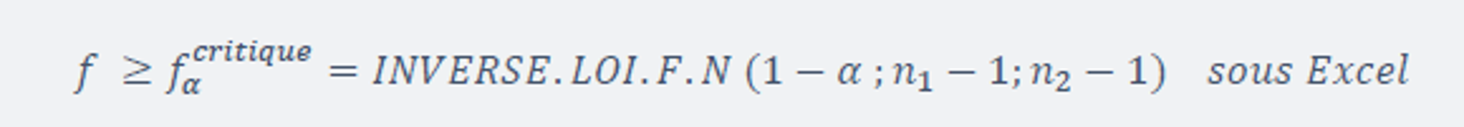
n1 représente le nombre de valeurs qui ont permis de calculer la variance du numérateur (répétabilité ou série en cours, suivant celui qui est le plus grand) et n2 celui du dénominateur.
Il n’est pas possible de développer ici la théorie des tests statistiques mais nous pouvons vérifier par simulation numérique que le test fonctionne effectivement.
Note : La valeur critique a été calculée pour un nombre de degrés de liberté égal à 10 000 (représente l’infini) pour la variance vraie (qui vaut strictement 1).
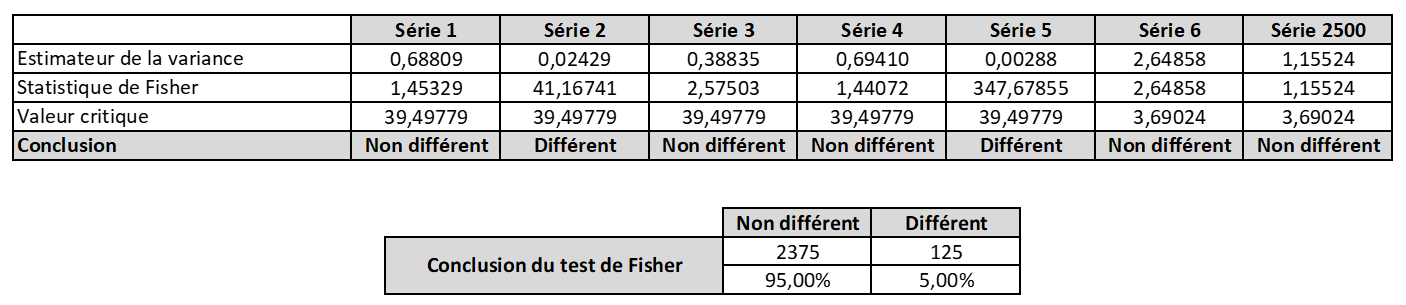
Mise en oeuvre du test de Fisher
Pour un niveau de confiance bilatérale à 95%, et alors que par simulation, tous les échantillons ont la même variance vraie, le test détecte 5% de séries qui semblent infirmer l’écart-type de répétabilité. C’est normal et inévitable, certaines conclusions du test seront erronées mais elles nous aident néanmoins à statuer de façon pertinente en fonction de la situation :
Situation 1 : Le test détecte une valeur plus petite que la valeur attendue (Cas des séries 2 et 5). Rien d’alarmant dans ce cas puisque la répétabilité est apparemment plus grande que celle de la série, l’incertitude n’est donc pas impactée.
Situation 2 : Le test détecte une valeur plus grande que la valeur attendue. Ce cas peut se produire :
- En cas d’une erreur de saisie dans les valeurs disponibles. Ce cas est évident et il suffit de corriger la valeur erronée;
- En cas d’un problème de fidélité de l’instrument en cours d’étalonnage (sa variabilité intrinsèque apporte plus de dispersion dans les mesures que la situation habituelle pour ce type d’instrument, type pour lequel la répétabilité a été étudiée). Dans ce cas, et pour confirmer ou infirmer, il suffit de refaire la série de mesures sur le point d’étalonnage concerné. Deux cas là encore :
- Soit le test détecte à nouveau une variance plus grande : l’instrument a alors de grandes chances d’avoir un problème de fidélité qu’il faut traiter au cas par cas. Il est en effet peu probable (mais pas impossible) que le hasard produise deux fois de suite une série détectée sans véritable problème sur l’instrument.
- Soit le test ne détecte pas la nouvelle série comme étant différente de la répétabilité et nous sommes alors dans la situation d’un test initial qui avait détecté « pour rien », du fait du niveau de confiance du test (Cas des « Différents » – qui ne le sont pas en réalité – du tableau 1)
Et pour finir
Lorsque toutes ses propriétés sont bien comprises, on peut aller encore plus loin en exploitant les données produites au cours des étalonnages pour estimer de façon très pertinente les effets de la répétabilité. Chaque point d’étalonnage, s’il y a au moins 2 répétitions, met en jeu la répétabilité du laboratoire. En fait, et si tout cet article a été construit sur de la simulation numérique, le laboratoire fait finalement la même chose, mais dans le monde réel … En accumulant des informations sur de nombreuses séries de 2, 3 ou n mesures dans son quotidien, le laboratoire dispose d’informations lui permettant de connaitre sa répétabilité de façon bien plus pertinente que lorsqu’il fait périodiquement 15 ou 30 mesures.
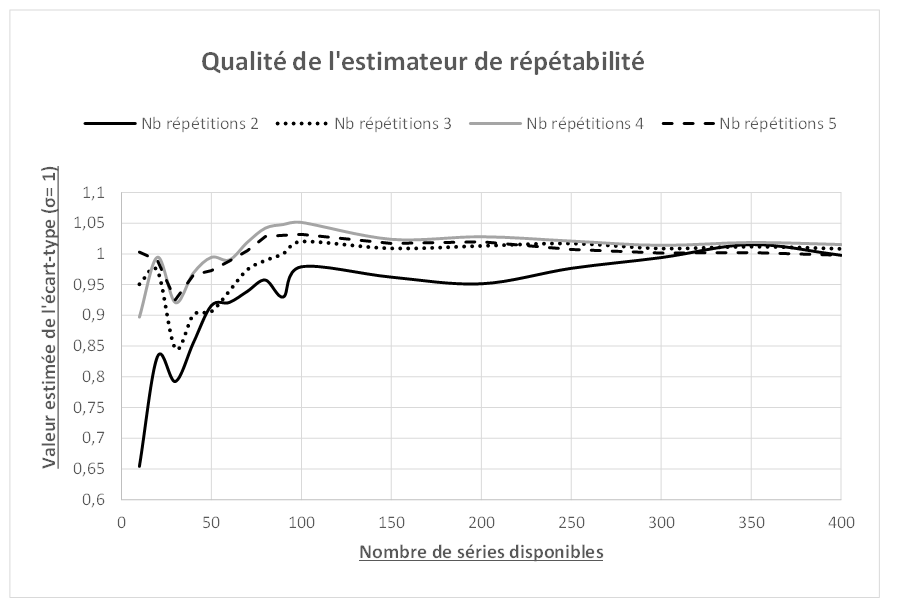
Figure 4 : Convergence des estimateurs d’écarts-types corrigés vers la valeur vraie
La figure 4 montre qu’en exploitant les séries disponibles lors des étalonnages, et en ne gardant que celles qui ne sont pas détectées comme possiblement différentes de la répétabilité, il est possible d’exploiter la moyenne de toutes les estimations d’écarts-types des séries et, en la corrigeant du facteur R vu précédemment, de converger vers la valeur vraie de la répétabilité. On peut également exploiter les variances et s’affranchir ainsi de la question du biais.
Dans la vraie vie d’un laboratoire, il est souvent rapide d’accumuler 200, 300, 500 séries ou plus et cette accumulation, lorsqu’on pratique la statistique de façon pertinente, permet d’en savoir plus que les fastidieuses études de répétabilité. Et si vous voulez essayer avec vos données, n’attendez pas les 300 prochaine séries, récupérez plutôt celles du passé 😉 !
Le raisonnement statistique pourrait nous amener beaucoup plus loin … Par exemple, en exploitant les noms des opérateurs à l’origine de chaque série, on peut pratiquer une ANOVA (Analyse de la variance), ANOVA qui pourrait nous indiquer que les opérateurs sont « sous contrôle », voire de détecter un opérateur dont les dispersions seraient plus importantes que celles de ses collègues. L’ANOVA pourrait également s’intéresser aux jours de la semaine (ont-ils une influence sur les résultats ?), aux effets environnementaux (pour peu que les mesures soient horodatées et des relevés de température/pression/hygrométrie disponibles et horodatés également).
On peut même détecter des biais de mesure, qu’ils viennent des étalons, des opérateurs, ou des conditions environnementales. Les laboratoires d’étalonnage ont une chance du point de vue statistique. Ils manipulent tous les jours des instruments provenant de constructeurs différents. Ces constructeurs cherchent tous (on peut l’espérer) à fabriquer des instruments « parfaits », c’est à dire des instruments sans erreur. S’ils ne peuvent évidemment pas réussir ce challenge à chaque fois, il semble très probable, qu’en moyenne, ils y arrivent. Autrement dit, l’instrument « moyen » de tous les instruments n’existent pas mais la moyenne des erreurs mesurées sur les instruments existe dans le laboratoire, et elle devrait théoriquement tendre vers 0. Dès lors, cette moyenne peut se présenter comme un étalon et avec un tel étalon toujours disponible, il est possible de faire tant de choses passionnantes : dérive des étalons du laboratoire, correction des biais éventuels, évaluation des biais opérateurs, … Nous avons déjà eu l’occasion de démontrer que cette approche pouvait être pertinente : https://fr.slideshare.net/JMP63/congrs-international-de-mtrologie-paris-2017
La statistique est au cœur du métier du métrologue, ce dernier devrait s’en convaincre et investir dans cette compétence. Sachant que tous ces calculs parfois fastidieux peuvent être réalisés automatiquement grâce aux technologies informatiques dont nous disposons désormais, elle ne lui réserve finalement que de bonne surprises. Essayez pour voir et vous serez vite convaincu !


