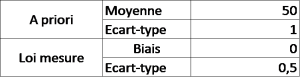Le métrologue sait aujourd’hui qu’il se doit d’évaluer les incertitudes de mesure. Même si cette mission est encore loin du quotidien du métrologue, la pression se fait de plus en plus ressentir, souvent par l’intermédiaire des auditeurs, quelques fois par les clients. Mais, une fois l’incertitude calculée, que faut-il en faire ? Il nous faut bien constater que dans la plupart des cas, elle ne sert à rien, elle n’est pas considérée et on peut comprendre pourquoi : on a toujours fait sans et ça va bien ainsi !

À force de GUM, de GUM S1, d’études R&R et d’ISO 5725, le métrologue a également compris que la statistique était au cœur des mesures. Lorsqu’elles sont systématiques, les erreurs peuvent être corrigées mais pour celles qui ne sont qu’aléatoires, il faut les considérer avec cette propriété troublante : on ne sait pas quelles valeurs elles vont prendre au moment de la mesure, on ne sait donc pas, et on ne saura jamais, qu’elle est la valeur vraie de l’entité mesurée. Et pourtant, comme dit un ami qui travaille dans le nucléaire, ce sont bien les champignons que nous mangeons, pas les mesures qu’on en fait. Ainsi, seules les valeurs vraies nous intéressent (les champignons sont-ils contaminés ?) et nous devons nous y résoudre, nous ne la connaitrons jamais…

Une chance dans notre (presque) malheur, les statisticiens nous aident largement pour comprendre et évaluer les phénomènes aléatoires. Ils ont démontré que lorsque plusieurs facteurs aléatoires élémentaires contribuent à un phénomène global, la somme des réalisations de chaque facteur se distribue suivant une loi de probabilité dite normale dont chaque propriété a été étudiée, décortiquée, analysée, publiée tellement il est fréquent de la rencontrer. Nous savons tout ou presque sur elle, mais dans la joie et l’allégresse d’avoir enfin trouvé une réponse à sa question existentielle (le GUM), il semblerait que le métrologue se soit un peu emballé…

Note : on appelle réalisation d’une variable aléatoire une valeur que prend le phénomène lorsqu’on l’observe à un moment donné. Par exemple, si je lance un dé, la réalisation de la variable aléatoire « Lancé de 1 dé » peut être 2, 1 ou 5 suivant la valeur sur laquelle le dé voudra bien s’arrêter. Une nouvelle réalisation pourra être la valeur 5, 6 ou 1, suivant là encore le hasard des choses…

La mesure est un processus comme un autre, qui met en jeu, pour résumer, les désormais fameux 5 M. Il est donc logique que l’incertitude de mesure, c’est-à-dire l’ensemble des erreurs de mesure possibles, puisse être considérée comme une variable aléatoire de loi de probabilité gaussienne, de moyenne 0 (ou de moyenne « biais », somme algébrique de tous les biais de tous les facteurs participants à la réalisation de la mesure si les effets systématiques ne sont pas corrigés) et d’écart type u_c (incertitude-type composée). Notons N(0;u_c) la loi de cette variable aléatoire.

Chaque mesure voit donc se produire une réalisation de la variable aléatoire N(0;u_c) autour de la valeur « vraie » de la grandeur d’intérêt. En effet, une valeur mesurée peut s’écrire sous la forme :

V_mes = V_vraie + e_mesure (1)

Où e_mesure est une réalisation de N(0;u_c).

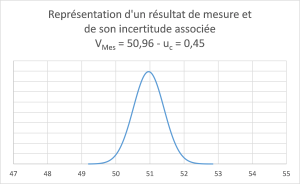
La représentation « graphique » que le métrologue se fait de l’incertitude de mesure, associée à la valeur numérique produite par son instrument de mesure, et parfois corrigée (cas des erreurs systématiques prises en compte), est la suivante :

Si cette représentation ne choque pas de prime abord (puisqu’elle est « traditionnelle »), il suffit de se poser une seule question pour la remettre en cause : la valeur mesurée est-elle vraiment, systématiquement, la plus probable ? Évidemment non, et il suffit pour s’en convaincre de répéter la mesure, ou de la faire faire à une autre personne, pour constater que le résultat de mesure varie… De ce fait, la valeur mesurée n’est pas la plus probable, la représentation graphique ci-dessus n’est pas correcte, et notre raisonnement, souvent appuyé sur ladite représentation graphique, est donc souvent erroné…

Une fois ce constat fait, le métrologue se trouve face à une autre question : comment faire autrement ?

Bayes a, en quelque sorte, donné la réponse, et il y a déjà longtemps. Dans la relation (1) ci-dessus, on a bien considéré l’erreur de mesure comme une réalisation d’une variable aléatoire, mais quid de la valeur vraie ? Dans bien des cas, l’entité d’intérêt (LE champignon choisi pour être mesuré ou LE patient qui demande à connaître sa glycémie) est également la réalisation d’une variable aléatoire ! Ce champignon est un champignon parmi les champignons disponibles, ce patient est l’un des patients possibles. Ainsi donc, la valeur « vraie » est elle aussi une réalisation d’une variable aléatoire du phénomène d’intérêt (la contamination des champignons ou la glycémie d’un patient). Notons donc Ph_Intérêt (μ;σ) la loi du phénomène d’intérêt duquel l’échantillon mesuré a été extrait.

Note : toutes les lois de probabilité ne sont pas définies par une moyenne et un écart type. De plus en plus souvent, nous devrons considérer des lois empiriques définies par leurs histogrammes des fréquences. Pour des raisons de simplification dans cet article, nous considérerons Ph_Intérêt (μ;σ) comme étant une loi normale de moyenne μ et d’écart type σ mais le raisonnement produit ici s’applique dans tous les cas.

Ce simple constat permet d’aborder la question de la mesure sous un angle différent. Une mesure est donc la conjonction de deux phénomènes aléatoires indépendants : une réalisation du phénomène d’intérêt Ph_Intérêt (μ;σ) + la réalisation de la variable aléatoire « Incertitude de mesure » N(0;u_c). Fort de cette nouvelle vision, et sous réserves de connaître les propriétés respectives de Ph_Intérêt (μ;σ) et de N(0;u_C), il est possible de calculer la probabilité d’obtenir le résultat trouvé suivant différentes configurations pour la valeur vraie et, par conséquent, pour l’erreur de mesure qu’il a fallu que le processus produise pour obtenir une valeur mesurée donnée. En effet, et suivant les propriétés statistiques bien connues, la probabilité de voir la conjonction de phénomènes indépendants se réaliser est égale au produit des probabilités de ces termes. Ainsi, la probabilité de trouver une mesure donnée est égale à la probabilité d’une valeur vraie donnée et d’une erreur de mesure associée égale à e_mes = V_mes – V_vraie (pour que la relation (1) soit respectée).

Considérons la situation suivante :

Note : dans le monde bayésien, on appelle la loi du process, qui « produit » la valeur vraie, la loi « a priori ». La loi résultant du produit des probabilités de la réalité et de la mesure s’appelle loi « a posteriori ».

Dans le cas où nous mesurons, dans un tel contexte, une valeur de 52, on peut estimer la probabilité d’un tel résultat pour différentes valeurs possibles de la valeur vraie :

Quelques valeurs de probabilité pour des valeurs vraies différentes

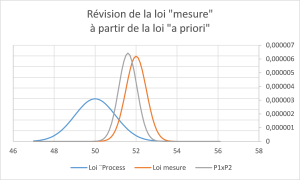
L’observation des lois en présence (A priori, Mesure et A posteriori) conduit au graphique suivant :

En ne disposant que de la valeur mesurée (52 ± 0,5 à 1 s), on ne peut rien dire de plus… En revanche, et en disposant d’une information « a priori » sur les valeurs vraies possibles (ce qui est souvent le cas finalement…), la valeur mesurée (52), l’incertitude associée (0,5) et les propriétés de la loi « a priori » ( Ph_Intérêt gaussien, de paramètres μ = 50, σ=1), il est possible de réviser la valeur mesurée pour obtenir :

• La valeur la plus probable sous-jacente : 51,6 (en lieu et place de 52)
• L’écart type de la loi « a posteriori », gaussienne elle aussi dans ce cas : 0,45 (en lieu et place de 0,5)

Avec cette nouvelle connaissance de la grandeur d’intérêt, établie sur la valeur la plus probable (et pas uniquement sur une valeur mesurée non fiable) et l’écart type associé, il est possible de quantifier la probabilité que valeur vraie soit ou pas au-delà de certaines limites (les champignons sont-ils contaminés ou le patient est-il malade). Ces évaluations de probabilité, puisqu’il s’agit bien de cela, deviennent des évaluations de risques, dès lors que la décision est prise de manger, ou de soigner, qui les champignons, qui le patient…

Voilà donc que se dessine un bel avenir pour la métrologie. Calculer une incertitude pour calculer une incertitude ne sert finalement pas à grand-chose (la preuve : nos pratiques actuelles). En revanche, connaître l’incertitude associée à un résultat et connaître suffisamment le phénomène d’intérêt duquel provient l’entité à mesurer (ce qui me parait finalement un minimum, les mesures doivent servir à cela !) permet d’améliorer sa connaissance de l’entité considérée, donc de mieux évaluer les risques liés à une décision la concernant !

Voilà donc tout tracé un projet ambitieux pour le métrologue, parfaitement compatible avec le Big Data qui se présente déjà comme l’un des fondements de l’usine du futur : mesurer convenablement pour réviser sa connaissance et tendre vers une certaine forme de vérité. Voilà, à mon sens, un chantier bien plus intéressant que celui de la gestion de dates sur des étiquettes…