La question de la dérive des instruments de mesure est une question essentielle en métrologie. L’étalonnage fait un « état métrologique » de l’instrument à la date de sa réalisation, mais qu’en sera-t-il demain, dans un mois, au terme de sa périodicité ? Si, dans le cas de certains instruments, cette question peut être convenablement traitée (notamment les instruments dits « à cote fixe », par exemple les étalons « physiques » et les calibres à limites), elle est plus délicate pour les instruments « mesureurs ». Le fascicule FD X07-014 distingue d’ailleurs ces deux cas, en évoquant les cas des instruments pour lesquels il est possible d’observer la dérive (du fait d’incertitudes d’étalonnage relativement faibles, ce qui est le cas en général pour les « cotes fixes ») et les autres (les mesureurs). Par ailleurs, dans le cas des « mesureurs », il convient de distinguer deux choses :

• la dérive de leur comportement systématique, dans le cas où le modèle qui donne la relation entre la valeur mesurée (notée y) en fonction de la valeur « vraie » (notée x) varie en fonction du temps ;
• la dérive de leur comportement aléatoire, c’est-à-dire le « résiduel » de justesse, qui se traduit par les écarts entre le modèle et les valeurs expérimentales observées lors des étalonnages. Ces écarts n’ont pas comme seule origine l’imperfection du modèle de l’instrument. Ils contiennent également l’erreur du modèle et les dispersions qui s’expriment lors de l’étalonnage (répétabilité du processus d’étalonnage notamment).

Modélisation d’étalonnage

Depuis le VIM de 2008, l’étalonnage ne se limite normalement plus à un tableau d’écarts entre valeurs mesurées et valeurs étalons. Il convient normalement d’établir la relation entre y et x de façon à exploiter l’instrument sur la totalité de son étendue (et pas uniquement sur les quelques points mesurés lors de l’étalonnage). Le Collège Français de Métrologie (C.F.M.) a publié un guide technique sur ce thème, guide auquel Deltamu a largement pris part. Une application Excel pour mettre en œuvre les préconisations du guide, nommée M-CARE est téléchargeable gratuitement  ainsi qu’une formation dédiée de 2 jours  : Nouvelle définition de l’étalonnage du VIM 3 : Utilisation du logiciel de modélisation M-CARE. À notre connaissance, peu de laboratoires proposent aujourd’hui cette prestation. Espérons que les industriels deviendront plus exigeants sur ce point et finiront par obtenir le calcul de la modélisation tel qu’il devrait être fourni en toute rigueur. En attendant, Excel permet déjà de faire simplement quelques calculs qui peuvent commencer à donner des informations importantes. Chacun a sûrement eu l’occasion d’utiliser les « courbes de tendance » pour obtenir des modélisations, soient affichées dans les graphiques, soient en « appelant » leurs paramètres dans la feuille de calcul (fonctions « PENTE », « ORDONNEE.ORIGINE », « DROITEREG »). Il est possible, en plus des valeurs des paramètres, d’obtenir les incertitudes sur l’estimation desdits paramètres suivant la méthode M.C.O. (Moindre Carrés Ordinaires, ou O.L.S.) pour en déduire, notamment, la significativité « physique » (lire à ce sujet : Exploitation des résultats d’étalonnage pour évaluer la part de l’instrument dans un bilan d’incertitude).

Dérive ou pas dérive ?

Il n’est pas aisé de démontrer une dérive d’un modèle obtenu suite à un étalonnage. En effet, les paramètres du modèle, calculés suite à un étalonnage, sont entachés d’incertitudes et ces incertitudes sont corrélées. D’ailleurs, et comme tout estimateur statistique, la réalité est « cachée » derrière les estimateurs et leurs incertitudes, ce qui rend difficile le fait de statuer sur une dérive entre deux étalonnages. En effet, les écarts apparents entre les derniers paramètres et les précédents sont-ils dus à une dérive ou simplement l’effet de l’incertitude ? Pour répondre à cette question essentielle, nous proposons une solution graphique simple et efficace. Pour simplifier les choses dans ce billet, nous nous limiterons au cas d’un modèle linéaire mais il est parfaitement possible de traiter de la même façon des modèles plus compliqués. Dans notre cas, on recherche donc, dans les résultats d’étalonnage, une relation linéaire entre y et x de la forme y = b₀ + b₁.x, sachant b₀ théoriquement proche de 0 et b₁ proche de 1. Pour statuer sur le fait que le modèle (défini par ses paramètres b₀, b₁) évolue ou pas, il est possible de construire un graphique en portant en abscisse la valeur b₁ (pente) et en ordonnée la valeur b₀ (ordonnée à l’origine). Les points seront classés dans l’ordre des étalonnages et reliés entre eux par un trait.

Cas d’une dérive non démontrée

Si, comme dans le graphique ci-dessous, les segments reliant deux points consécutifs se croisent « sans cesse », on peut conclure que la différence apparente des coefficients est essentiellement le fait des incertitudes. De ce fait, l’instrument ne dérive pas (ce qui méritera d’être confirmé, ou infirmé, lors des étalonnages à venir) et le facteur « dérive » des bilans des causes d’incertitude des processus qui l’utilise pourra être considéré comme « négligeable ».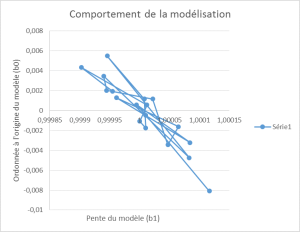

Cas d’une dérive probable

À l’inverse, lorsque les segments ne se coupent pas (ou presque), il y a de bonnes raisons pour penser que l’instrument dérive : 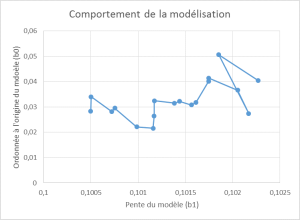Dans ce cas, il est alors possible de modéliser le comportement des paramètres b₀ et b₁ (dans le cas d’une droite, mais il en est de même sur des polynômes de degré supérieur). Évidemment, cette modélisation n’a pas pour vocation d’être rigoureusement prédictive. Néanmoins, elle permet d’estimer, et nous allons maintenant voir comment, la part de la dérive dans un calcul d’incertitude.

Modélisation du comportement de b₀ et b₁ au cours du temps

Cette modélisation peut être faite tout simplement, avec la méthode O.L.S. (d’Excel), même si on pourrait aller plus loin en considérant les incertitudes sur les b₀ et b₁ obtenus au fil des étalonnages. Pour cela, on portera en abscisse la date des étalonnages et en ordonnée le paramètre concerné (b₀ puis b₁). La fonction « DROITEREG » calcule, dans ce cas, les paramètres en transformant les dates en « nombre de jours ». Les paramètres sont alors donnés en « variation par jour ».

Comportement de b₀ : 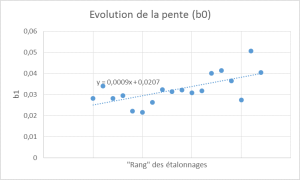Comportement de b₁ : 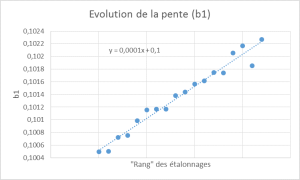Dans cet exemple « simulé », nous disposons d’un grand nombre d’étalonnages, donc de points « expérimentaux ». La modélisation est donc très performante. Dans le cas où nous disposons de moins d’étalonnages, elle sera moins fiable mais elle s’enrichira au fur et à mesure des étalonnages réalisés. Il conviendra donc de tenir compte de ce manque d’information dans l’interprétation des phénomènes et dans les estimations qui en découlent.

Estimation du terme de « dérive » à considérer dans un calcul d’incertitude

Lorsqu’un modèle linéaire dérive, ledit modèle (la « droite ») obtenu à la date du dernier étalonnage  va évoluer dans le temps. Le modèle « au moment de la mesure » se distingue donc chaque jour un peu plus du modèle utilisé (c’est à dire le dernier modèle connu, obtenu lors du dernier étalonnage, appelé « modèle à t0 » ci-après). On peut facilement s’imaginer deux droites sécantes, l’une « fixe » (« Correction t0 » dans la figure ci-dessous) et l’autre qui « s’écarte » de cette position d’origine du fait de la dérive. Plus le temps passe, plus l’écart de modèle (entre modèle à t0 et celui au moment de la mesure) augmente … Les deux modèles n’étant pas forcément parallèles (Sauf dans le cas particulier où seul b₀ évoluerait), l’écart entre les 2 modèles (Modèle t0 et modèle réel au moment de la mesure) dépend de la quantité mesurée (donnée en abscisse). 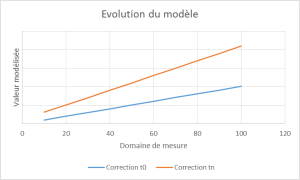Ici, nous sommes donc confrontés à un phénomène de type systématique. En effet, l’écart entre le modèle à t₀ et celui à t_n n’a rien d’aléatoire. Il est fonction de la valeur de X, dans le domaine de mesure. Petit parallèle pour comprendre …

Dans un laboratoire par exemple, on considère comme aléatoire une température en considérant que, dans le temps, elle est comprise entre deux limites. En fait, en un temps donné, elle est ce qu’elle est et on pourrait la connaître, et donc en tenir compte. Dans notre esprit, ce qui rend la température du laboratoire aléatoire, c’est qu’on fait un calcul d’incertitude qui exprime la qualité d’un résultat quelque soit le jour de la mesure. C’est donc le moment de la mesure qui donne le caractère aléatoire de la température, et non la température elle-même.

Dans le cas qui nous intéresse, la situation est à peu près la même. En effet, l’écart sera ce qu’il sera en une valeur donnée du domaine de mesure mais, comme on fait un calcul d’incertitude quelle que soit la valeur dans le domaine de mesure, on peut considérer que ce « quelle que soit » donne le caractère aléatoire à l’écart. Pour évaluer le terme lié à la dérive potentielle du moyen, et fort des explications précédentes, nous proposons de calculer les écarts entre les deux corrections (t₀ et t_n) sur des points répartis sur la totalité du domaine de mesure, puis de calculer la moyenne et l’écart-type des écarts obtenus. Ces deux termes, moyenne et écart-type, sont la contribution de la dérive dans l’incertitude du processus de mesure. La moyenne peut être intégrée dans le calcul d’incertitude en la considérant, par exemple, comme se distribuant suivant une loi uniforme (donc en la divisant par racine(3)). L’écart-type est considéré directement dans le bilan. 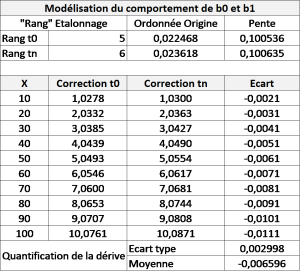Évidemment, moins nous disposons d’étalonnages pour statuer sur la dérive (donc pour modéliser le comportement des paramètres b₀ et b₁ dans le temps), moins les termes calculés (moyenne et écart-type) sont fiables. Pour prendre compte ce manque d’information, on pourrait par exemple considérer les incertitudes associées aux paramètres de modélisation du comportement de b₀ et de b₁ en faisant les mêmes calculs d’écarts sur des points répartis sur la totalité du domaine de mesure avec une combinaison défavorable pour de (b₀, b₁) à t₀ et de (b₀, b₁) à t_n. Remarque importante : pour faire ces calculs, il est impératif de considérer, pour les paramètres b₀, b₁ à t₀, les paramètres modélisés qui ne sont pas forcément les paramètres calculés à partir des derniers points d’étalonnage. Par cette méthode, il est possible de choisir une périodicité adaptée. Il suffit en effet de la choisir en faisant en sorte que le poids de la dérive soit acceptable dans l’incertitude des processus qui utilisent le moyen concerné.