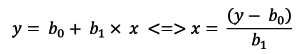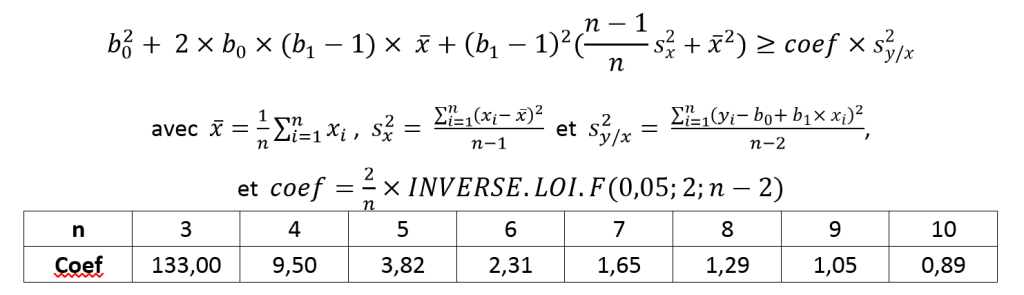Exploitation des résultats d’étalonnage pour évaluer la part de l’instrument dans un bilan d’incertitude
Comment exploiter des résultats d’étalonnage ? Voilà une question qui devrait être traitée depuis plus de 20 ans mais qui reste pourtant en suspens, encore de nos jours…
Si tous les métrologues d’entreprise et tous les étalonneurs ont bien compris l’exigence des auditeurs en terme de respect d’une périodicité souvent arbitraire, il est stupéfiant de constater que la façon d’interpréter des résultats d’étalonnage reste floue… Tous les métrologues ont de nos jours des logiciels de métrologie qui leur permettent d’établir des plannings et des indicateurs, mais que font-ils des informations disponibles dans les certificats d’étalonnage ?
La réponse la plus classique tient souvent en une phrase : « on ne fait pas des étalonnages, on fait des vérifications ! ». Rappelons, dans un premier temps, qu’une vérification impose (dans la très grande majorité des cas, même s’il existe des exceptions) un étalonnage préalable. Et pire, la vérification est souvent effectuée par rapport à une norme souvent totalement inadaptée au besoin spécifique de l’industriel qui se sent pourtant concerné, par la force des pratiques qui ont fini par s’imposer sans forcément être pertinentes…
En 2008, le VIM a évolué. Il a défini un étalonnage (définition 2.39) de la façon suivante :
Étalonnage : opération qui, dans des conditions spécifiées, établit en une première étape une relation entre les valeurs et les incertitudes de mesure associées qui sont fournies par des étalons et les indications correspondantes avec les incertitudes associées, puis utilise en une seconde étape cette information pour établir une relation permettant d’obtenir un résultat de mesure à partir d’une indication.
NOTE 1 Un étalonnage peut être exprimé sous la forme d’un énoncé, d’une fonction d’étalonnage, d’un diagramme d’étalonnage, d’une courbe d’étalonnage ou d’une table d’étalonnage. Dans certains cas, il peut consister en une correction additive ou multiplicative de l’indication avec une incertitude de mesure associée.
NOTE 2 Il convient de ne pas confondre l’étalonnage avec l’ajustage d’un système de mesure, souvent appelé improprement « auto-étalonnage », ni avec la vérification de l’étalonnage.
Le Collège Français de Métrologie s’est rapidement saisi de cette évolution pour traiter de cette évolution. Il a produit un guide nommé « Application du nouveau concept d’étalonnage du VIM 3 » qui permet de répondre à cette nouvelle définition. Il propose également un logiciel téléchargeable gratuitement, M-CARE, qui permet de réaliser les calculs proposés. Deltamu propose également en complément une formation dédiée de 2 jours : Nouvelle définition de l’étalonnage du VIM 3 : Utilisation du logiciel de modélisation M-CARE.
Force est de constater qu’à ce jour, alors que le VIM fête ses 7 ans cette année, rares sont les étalonneurs qui appliquent cette définition. Évidemment, il faut reconnaître quelques difficultés mathématiques et, finalement, tant que les industriels ne demandent rien…
Quelques mots de théorie
Il existe dans la littérature de nombreuses stratégies pour trouver un modèle à partir de données expérimentales. La plus classique, utilisée par Excel, repose sur une stratégie dite des « moindres carrés ». Apparemment simple, l’approche par les moindres carrés recouvre différentes possibilités plus ou moins élaborées :
– Moindres carrés ordinaires (O.L.S.) qui ne traite que des valeurs de x et de y observées, sans tenir compte des incertitudes associées. Pour être utilisable, cette technique demande que quelques conditions soient respectées :
- Pas d’incertitude en x (ce qui n’est jamais le cas lors d’un étalonnage, mais on peut parfois la supposer négligeable),
- Incertitude identique sur les y (ce qui est rarement le cas en étalonnage car il est fréquent que l’incertitude soit proportionnelle à la valeur de x – cas des incertitudes qui s’expriment en %),
- Pas de covariance entre les incertitudes en y (ce qui est rarement le cas lors des étalonnages, pour les raisons évoquées ci-avant.
– Moindres carrés pondérés (W.L.S.) qui prend en compte la « qualité » des données disponibles en y, notamment en associant des poids différents, inversement proportionnels à l’incertitude sur chacun des y (qui doivent donc être connus), à chaque valeur de y pour le calcul des coefficients du modèle. Là encore, quelques conditions :
- Pas d’incertitude en x (ce qui n’est jamais le cas lors d’un étalonnage, mais on peut parfois la supposer négligeable),
- Pas de covariance entre les incertitudes en y (ce qui est rarement le cas lors des étalonnages, pour les raisons évoquées ci-avant).
– Moindres carrés généralisés (G.L.S.) qui prend en compte la « qualité » des données disponibles en x et en y. Dans cette méthode, les covariances ne sont pas prises en compte.
– Méthode dite G.G.M.R. (Generalized Gauss Markov Regression) qui prend en compte la totalité de l’information, c’est-à-dire les incertitudes en x, en y et toutes leurs covariances éventuelles.
Cette liste n’est donc pas exhaustive. D’autres approches, très différentes, sont disponibles dans la littérature. On peut notamment citer les techniques dites de « maximum de vraisemblance » ou « d’inférence bayésienne ».
Dans tous les cas cités ci-avant, tout type de modèle (ou fonction de mesure) peut être estimé. Elles ne se limitent pas aux simples droites et peuvent permettre d’estimer tout type de polynômes notamment.
Ces différentes techniques ne se limitent pas à estimer les coefficients du modèle. Elles permettent également d’estimer l’incertitude sur lesdits coefficients, incertitudes qui proviennent du fait que les données d’entrée, notamment les y dans tous les cas, ne sont pas parfaites.
Quelle stratégie choisir ?
Cette question est essentielle en matière d’étalonnage. Lorsqu’on est attentif à la réalité des conditions d’étalonnage et aux conditions d’utilisation de telle ou telle approche, seule la technique dite G.G.M.R. correspond au contexte. On peut souligner que l’application M-CARE propose une solution pour calculer la matrice de variances/covariances sur les données disponibles, ce qui est un prérequis de la méthode G.G.M.R.
Force est de constater que dans le quotidien des laboratoires, la méthode la plus utilisée est la méthode proposée par Excel, à savoir la méthode O.L.S. De plus, rares sont les laboratoires qui vont au bout de la démarche en estimant, en plus des coefficients, leurs incertitudes associées. Ces incertitudes doivent pourtant ensuite être considérées dans le calcul d’incertitude globale des processus de mesure auxquels l’instrument participe, dans le cas, évidemment, où une modélisation est appliquée à la mesure brute donnée par le moyen.
Par ailleurs, les techniques des moindres carrés permettent de calculer le modèle qui donne y (mesure) à partir de x (étalon). Or, en métrologie, c’est le modèle inverse qui est utile, celui qui donne x (valeur « vraie ») en fonction de y (valeur physiquement mesurée). Cette inversion du modèle impose une précaution essentielle car il ne suffit pas « d’inverser les colonnes » pour que ça fonctionne (même si les mathématiques – Excel – donnent toujours des valeurs…) !
Les points « clefs » des modélisations
On peut prendre acte que les conditions d’application des méthodes de régression ne sont pas respectées mais il faut néanmoins s’imposer quelques précautions :
- Le sens du modèle :
Pour les calculs des coefficients, il est impératif de choisir pour valeurs des « x » (c’est-à-dire en abscisse) les valeurs connues avec le moins d’incertitude et ce ne sont pas toujours les valeurs étalons. Lorsque des solutions filles sont élaborées par dilution d’une solution mère, il n’est pas rare que les incertitudes liées aux dilutions (et très corrélées entre elles) soient plus importantes que les incertitudes sur la lecture (cas des densités optiques par exemple). En pratiquant ainsi, le modèle est parfois directement dans le bon sens (de y vers x), parfois dans le mauvais (de x vers y). Dans le second cas, il convient d’inverser mathématiquement le modèle estimé. Dans le cas d’une droite, on trouve :
Évidemment, dans le cas d’un modèle plus complexe, l’inversion n’est pas toujours simple. La méthode G.G.M.R. n’est pas sujette à cette condition sur les incertitudes en x. Elle peut donc se présenter comme une alternative en cas de modèles trop complexes.
- L’opportunité de la correction :
Dans le cas simple d’un modèle linéaire de type y = x (cas des instruments de mesure qui mesurent directement), il ne suffit pas de trouver une valeur pour b0 ≠ 0 et/ou une valeur de b1 ≠ 1 (b0, ordonnée à l’origine du modèle, b1 la pente) pour démontrer l’existence d’un modèle.
Par extension, si le modèle est différent de y = x :
- Par exemple y = M(b0 ,b1, …, bn, x) avec des coefficients b0, b1, …, bn connus « a priori », par exemple la moyenne des coefficients habituellement trouvés lors des étalonnages précédents
Il ne suffit pas de trouver b0NouvelEtalonnage ≠ b0Apriori, b1NouvelEtalonnage ≠ b1Apriori, … bnNouvelEtalonnage ≠ bnApriori pour statuer sur l’opportunité de remplacer les anciens coefficients par les nouveaux.
- La prise en compte des résidus au modèle
Lorsqu’un modèle est recherché, il est rare qu’il passe par tous les points expérimentaux. La différence entre l’ordonnée y (souvent, mais parfois suivant le sens « imposé » par les incertitudes) et l’ordonnée modélisée ym = M(b0, b1, …, bn, x) se nomme « résidu ». Un résidu existe donc pour chaque valeur de x . Il « contient » des erreurs de différents types :
- L’erreur liée au modèle choisi : si vous modélisez un phénomène réellement polynomial avec une droite, le résidu « contient » l’écart entre la réalité (polynomiale) et le modèle (fixé par hypothèse mais pas « conforme » à la réalité),
- La fidélité de l’instrument de mesure étalonné, c’est-à-dire ses propres erreurs locales qui font que sa réalité ne pas pas être réduite à une forme analytique simple (droite ou autres modèles),
- La répétabilité qui s’est exprimée sur le y au moment même de la mesure.
Note : Les résidus ne contiennent pas les effets des facteurs d’incertitude d’étalonnage qui n’ont pas eu l’opportunité de varier pendant l’étalonnage. Par exemple, si la température, identifiée comme un facteur d’influence de l’incertitude d’étalonnage, n’a pas (ou peu) varié pendant l’étalonnage et qu’elle n’est pas égale à la valeur de référence, cela génère un écart qui est à l’origine d’une erreur qui sera la même (en absolu ou en relatif) dans tous les y. Elle ne se verra donc pas dans les résidus mais se « glissera » dans les paramètres du modèle. Il s’agit là de l’effet des covariances que la méthode G.G.M.R. prend en compte dans ses calculs.
À ce stade, on peut donc dire que la variance des résidus est un majorant des effets « fidélité » et « erreur de modèle » de l’instrument. Il est d‘ailleurs d’usage d’observer la distribution des résidus qui doit être gaussienne si le modèle est conforme à la réalité et éviter ainsi des erreurs de modèle trop grossières.
Des techniques approximatives acceptables
La question de la significativité des coefficients est une question traitée par les statisticiens mais souvent oubliée. Elle s’appuie sur un test de Fisher qui permet de comparer les anciennes et nouvelles valeurs des coefficients en tenant compte des incertitudes associées et de leurs covariances. Même si cette difficulté n’est pas insurmontable, notamment dans le cadre d’une droite, ce test n’est pas trivial et demande quelques calculs pouvant repousser, ceci explique probablement cela. Le guide du C.F.M. aborde cette question sous l’angle de la « signature d’un processus d’étalonnage », concept développé et exposé depuis longtemps par Deltamu.
Cas des modèles linéaires
Dans le cas du modèle simple y = x, l’approche théorique est abordable avec quelques calculs aisément accessibles.
Soient des résultats d’étalonnage qui conduisent à n couples (xi, yi) où xi représente les valeurs étalons ou les valeurs mesurées (suivant l’importance des incertitudes sur les unes – étalons ou les autres – valeurs mesurées) et yi les autres. La relation supposée est yi = b0 + b1.x . Le résultat ci-dessous n’est valable en toute rigueur que si les paramètres b0 et b1 sont obtenus en appliquant la régression O.L.S.
Le modèle linéaire sera significativement différent de y = x si :
Si la correction n’est pas significative, l’écart-type des résidus s2y/x sera une estimation acceptable de la performance (l’incertitude) du moyen de mesure dans un bilan de causes d’incertitude.
Si la correction est significative, il convient alors d’estimer l’incertitude liée à la correction en appliquant la loi de propagation du GUM. Ceci suppose d’estimer les incertitudes sur les coefficients du modèle avec comme seule solution statistiquement acceptable la méthode G.G.M.R. mise en œuvre par M-CARE.
Approximation pour les modèles ≠ (y = x)
Les calculs proposés par la théorie statistique peuvent, dans ces cas-là, devenir compliqués. Vous pourrez trouver des informations dans : « P.H. Cornillon, E.M. Lober, Régression – Théorie et application, Ed Springer ».
En première approximation, on peut estimer la pertinence de la correction (ou du modèle) en comparant les paramètres obtenus à partir des données du nouvel étalonnage et les paramètres utilisés jusque-là (ou « a priori »). Excel ne met en œuvre que la méthode O.L.S. dans le cadre des calculs de moindres carrés et la fonction DROITEREG retourne les paramètres et leurs incertitudes, en l’utilisant sous forme de « fonctions matricielles ».
Pour un polynôme à l’ordre n, la syntaxe de la fonction est la suivante :
DROITEREG(yconnus;xconnus^{1.2.3….n} ;VRAI ;VRAI)
Pour que cette fonction retourne tous les résultats, il convient :
- de taper la formule ci-dessus, en faisant référence aux valeurs de Y et de X, dans une cellule (ici la cellule A8 pour un exemple à l’ordre 3) ;
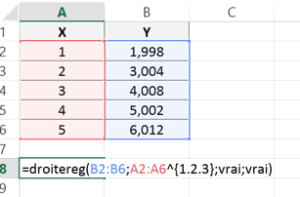
- de sélectionner la cellule qui contient la formule et autant de cellules que nécessaire pour contenir les paramètres (4 cellules en tout, si un polynôme de degré 3 est attendu) à droite de la cellule qui contient la formule plus les 2 lignes du dessous, puis taper F2 ;
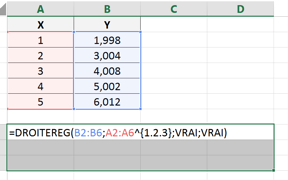
- Taper Ctrl + Maj + Entrée pour obtenir les valeurs des coefficients, dans l’ordre décroissant, et leurs incertitudes associées dans la ligne du dessous et du coefficient de détermination r2 dans la première cellule de la 3e ligne.
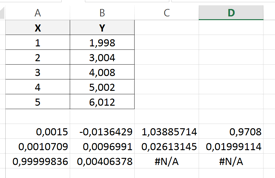
À ce stade, le coefficient de détermination r2, donné par Excel dans la 1re cellule de la 3e ligne (0,9999… dans l’exemple) permet de valider que le degré du polynôme permet de décrire correctement les données expérimentales.
La 2e ligne donne les incertitudes types sur chacun des paramètres. Il est ainsi possible de comparer chacun des nouveaux coefficients (b0, b1, …) aux coefficients précédents (a priori), suivant la formule ci-dessous, pour statuer sur leur différence ou pas.
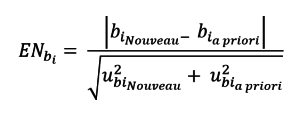
Dans le cas où aucun paramètre n’est statistiquement différent du paramètre « a priori », le nouveau modèle n’est pas différent du modèle « a priori ». Il est alors possible de considérer les nouveaux paramètres pour réviser les paramètres « a priori », par le biais d’une moyenne pondérée des paramètres par exemple. Dans le cas contraire, le nouveau modèle décrit par l’ensemble de ces nouveaux paramètres peut être utilisé mais il conviendrait d’utiliser la méthode G.G.M.R. pour le traiter convenablement.
Cette méthode simplifiée ne permet pas de prendre en compte les covariances entre les paramètres du modèle alors qu’elles sont souvent conséquentes. Du coup, un nouveau modèle peut être considéré comme non différent du modèle « a priori » alors qu’il l’est en réalité. L’utilisation de la méthode G.G.M.R. permet de limiter cette potentielle erreur de jugement.
Note : La fonction matricielle DROITEREG retourne les incertitudes types sur les paramètres des modèles. De ce fait, l’application de la loi de propagation des incertitudes du GUM est parfaitement réalisable.
Conclusion
Cet article a pour objectif de sensibiliser à la problématique de la modélisation, qui ne peut pas se résumer à l’ajout d’une courbe de tendance via Excel. Le monde de la métrologie est le monde des incertitudes, et tous nos calculs en sont entachés.
Le métrologue doit prendre conscience que chaque mesure, chaque paramètre calculé à partir de mesures ne sont finalement que des estimations de la réalité recherchée. Et qui dit « estimation » dit « test », c’est-à-dire la confirmation ou l’infirmation d’une hypothèse…