La métrologie légale a raison, et les métrologues industriels qui se contentent d’utiliser des EMT se trompent lourdement. Discutons …

La métrologie légale a inventé les Erreurs Maximales Tolérées (EMT) et les périodicités calendaires. Elle a raison d’avoir développé ces stratégies qui satisfont pleinement leur objectif : garantir la loyauté des échanges commerciaux. Il ne s’agit pas pour elle, en effet, d’estimer, pour chaque transaction commerciale, l’incertitude de mesure et de calculer un risque, client ou fournisseur, suivant la norme NF / ISO/IEC Guide 98-4. On sait que chaque mesure est fausse et il « suffit » donc de faire en sorte que l’erreur qui se produira soit « équitable », c’est à dire « raisonnable » eu égard à la situation et qu’elle n’ait pas de préférence, ni pour le vendeur, ni pour l’acheteur.

En partant d’un constat simple suivant lequel seul l’instrument de mesure peut être à peu près maitrisé (tous les commerçants ne vont pas passer une accréditation COFRAC 😉), la métrologie légale a décidé de fixer par décret des conditions de vérification (protocole et qualité des étalons) identiques pour tous les instruments d’un même type. Ainsi, elle peut sans problème évoquer le concept d’« erreur de mesure » (écart entre la valeur de l’étalon et la valeur indiquée par l’instrument). Elle peut également définir le concept d’« erreur maximale constatée » (plus grande des erreurs observées sur l’ensemble des points étalonnés) même si cette dernière ne donne aucune information factuelle sur l’amplitude de celle qui aurait pu être observée si on avant vérifié toutes les autres valeurs possibles que peut mesurer l’instrument. L’acheteur et le vendeur sont donc soumis au hasard de la graduation sur laquelle tombera l’instrument, étant entendu qu’il est peu probable que ce soit l’une des graduations étalonnées. Le risque demeure donc, mais il n’est pas vital …

Une fois ces concepts acceptés et compris, on peut, sans se soucier des incertitudes d’étalonnage (inévitables), déclarer une conformité par rapport à une EMT (fixée par décret) par une simple comparaison algébrique. Si l’erreur la plus grande observée et égale ou plus petite que l’EMT, l’instrument est « conforme ». Dans le cas contraire, il est « non conforme ». Qu’importe finalement[1] ce qui se passe sur les points non observés, on définit la loyauté comme étant le respect de ces exigences qui sont, par ailleurs, validées périodiquement suivant une périodicité fixée par le décret elle-aussi. Si la vérification est « conforme », elle est inutile et on la paye pour rien. Si elle est « non conforme », elle intervient trop tard et le client ou le commerçant ont pu être « volés ». Dans les deux cas, nous ne sommes pas optimaux mais c’est le prix à payer pour garantir la loyauté ! En effet, la loyauté est sauve car si l’instrument est « non conforme », il peut l’être au bénéfice du client ou du commerçant, sans préférence a priori. On parle alors de « partage des risques » mais de risques bien dérisoires puisque nous ne sommes pas dans des situations vitales !

L’ISO 9000, à ses débuts, a mis le sujet de la « métrologie » sur la table des industriels. Elle exprimait alors des exigences très claires et pertinentes[2] en matière de métrologie mais je crois pouvoir affirmer que la (réelle) difficulté du sujet a rebuté tout le monde (ou presque). Aussi, et dans une forme de consensus implicite, audités et auditeurs se sont contentés, pour le premier de vérifier à des dates arbitraires des instruments de mesure suivant des exigences la plupart du temps pas faites pour lui et les seconds de vérifier que les premiers faisaient bien leur « travail ».

Pour avoir occupé des responsabilités de tout premier plan dans de nombreux laboratoires prestataires, j’ai pu finalement constater que seules les questions de la conformité à la norme (ou aux spécifications constructeurs[3]) et de l’accréditation COFRAC étaient importantes. L’origine des EMT demandées et leur pertinence eu égard au besoin spécifique de chacun de mes clients[4] de l’époque n’étaient quasiment jamais abordée.

Dans le monde industriel, contrairement au monde de la métrologie légale, on ne cherche pas à garantir la loyauté, mais la conformité, c’est-à-dire la fonctionnalité, des entités livrées aux clients. Or, et puisque toutes les mesures sont fausses par nature, la décision de conformité fait forcément naitre un doute. On risque de livrer une entité conforme alors qu’elle ne l’est pas en réalité ou de rebuter une entité conforme en pensant qu’elle ne l’est pas. Ces doutes se transforment en risques dès lors que la décision est prise : risque client dans le premier cas, risque fournisseur dans le second. Et la norme NF ISO/IEC Guide 98-4 donne désormais une méthode objective pour évaluer ces risques …

Patatrac dans le domaine de la métrologie industrielle !

Je considère depuis longtemps ces histoires d’EMT comme totalement stupides pour le monde industriel, nonobstant l’avis plus que majoritaire d’un système qui s’est construit sur ce paradigme en en oubliant l’origine. Lorsque nous sommes dans un avion, on se moque bien de la loyauté. On exige la fonctionnalité pour pouvoir être rassuré sur le fait qu’il atterrira dans de bonnes conditions !

Il suffit de faire quelques calculs de risques, tels que proposés par le guide 98-4, pour comprendre la stupidité dénoncée ci-dessus. En effet, et pour résumer très simplement[5] le propos qui mériterait de longs développements mathématiques, chacun comprend, à la lecture du Tableau 1, que l’instrument 1 n’a rien à voir, en termes de caractéristiques métrologiques, avec l’instrument 2 malgré le fait qu’ils présentent, tous les deux, la même « erreur maximale observée ».

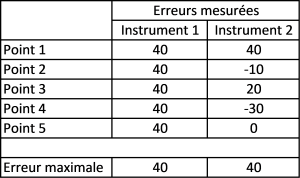
Tableau 1 : Exemples d’erreurs mesurées au cours d’étalonnage

L’instrument 1 semble présenter une erreur de type systématique qui, si elle n’est pas corrigée, provoque un biais de l’incertitude de mesure du processus qui l’utilisera. Ce biais aura un effet bien différent, lors du calcul des risques, que les erreurs que semblent produire l’instrument 2 qui, elles, paraissent de type aléatoire.

Biais ou dispersion, impact sur les risques

Pour illustrer l’impact de ces 2 situations, on peut imaginer un processus de mesure dont la seule composante de l’incertitude serait l’erreur due à l’instrument. On négligera donc notamment, pour comprendre, les incertitudes d’étalonnage. Par ailleurs, et pour respecter le guide 98-4, on imaginera que nous n’avons aucune connaissance sur la loi a priori. Dans ce cas, la loi a posteriori est égale à la loi des mesures[6].

Pour l’instrument 1 qui présente une erreur systématique, le risque d’une erreur de décision est égal à 0% tant que le biais non corrigé est inférieur à la « distance » qui sépare la valeur mesurée de la limite d’acceptation (Figure 1). Il est égal à 100% si le biais est supérieur à la distance entre la valeur mesurée et la limite d’acceptation (Figure 2).

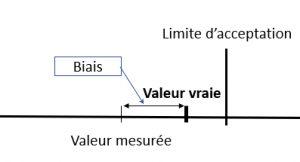
Figure 1 : Situation de risque client égal à 0%

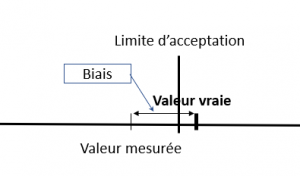
Figure 2 : Situation d’un risque client égal à 100%

Pour l’instrument 2, dont le comportement est de type aléatoire, la situation de la Figure 1 devient celle présentée en Figure 3. Dans ce cas, le risque client est approximativement égal à 0% (versus rigoureusement égal à 0% dans le cas de la Figure 1).

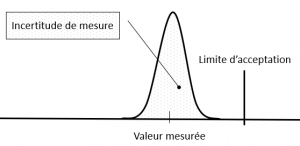
Figure 3 : Situation de la figure 1 avec une erreur de type aléatoire

En revanche, et dans la même situation de valeur mesurée que celle présentée en Figure 2, le risque client est bien inférieur au 100% (Figure 4) !

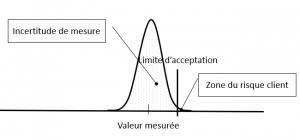
Figure 4 : Situation de la figure 2 avec une erreur de type aléatoire

Ces situations permettent de comprendre qu’une déclaration de conformité à une EMT n’a aucun sens réel si on s’intéresse à la seule chose qui, finalement, motive la fonction de métrologue industriel : estimer les risques liés aux décisions qui seront prises sur la base de mesure. Il y a donc une forme d’escroquerie à continuer à faire croire qu’une vérification est une action pertinente en métrologie, en tout cas tant qu’on ne fait pas la distinction entre la part systématique et la part aléatoire des erreurs de l’instrument.

L’EMT différenciée : Vers une approche plus satisfaisante …

En réalité, l’erreur d’un instrument est toujours une composition d’un effet aléatoire et d’un effet systématique. En modélisant les résultats d’étalonnage tel que demandé par la définition même de l’étalonnage suivant le VIM 2008 (Phase 2) et en suivant par exemple les préconisations du guide du Collège Français de Métrologie qui traite de cette question[7], la distinction entre la part aléatoire et la part systématique des erreurs de l’instrument devient possible.

Dans ce nouveau cadre, le résultat d’un étalonnage devrait se présenter sous la forme d’un vecteur de paramètres d’un modèle (les coefficients b₀ et b₁ d’une correction linéaire par exemple), d’une matrice de variances/covariances des coefficients (qui permet ensuite d’appliquer la loi de propagation du GUM pour estimer une partie de l’incertitude de modélisation) et de la variance des résidus (qui complète l’incertitude de modélisation en permettant d’intégrer les effets qui ne sont pas expliqués par le modèle retenu).

Présentés sous cette forme, les résultats d’un étalonnage se décomposent en une part systématique (qu’on corrige ou qu’on ne corrige pas – Composante 1) et une part aléatoire (l’écart-type des résidus – Composante 2) qui ne peut pas être corrigée puisqu’aléatoire. La déclaration de la conformité d’un instrument par rapport à une EMT doit donc s’établir en tenant compte de ses deux composantes, eu égard au risque induit …

L’EMT doit permettre de garantir les risques !

Si l’objectif d’une déclaration de conformité d’un instrument de mesure est de garantir un risque (sinon à quoi pourrait-elle bien servir ?), il est impératif d’intégrer l’impact de ses deux composantes sur ledit risque. Et chacun comprendra que plus nous sommes éloignés de la limite acceptable, plus nous avons de la place pour la partie aléatoire de l’instrument[8].

Le petit tableau ci-dessous montre comment évolue le couple biais/dispersion pour une même EMT en fonction d’un risque fixé.

Tableau 2 : Couple biais/variance pour un risque donné

Ce tableau peut être présenté graphiquement en portant en abscisse le biais et en ordonnée l’écart-type. On obtient alors une forme en demi-triangle, sachant évidemment qu’il y a une symétrie par rapport à l’axe des ordonnées quand l’EMT est donnée en ± (Figure 6).

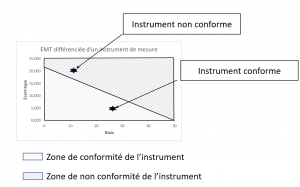
Figure 5 : Représentation d’une EMT différenciée

Dans la Figure 5, on matérialise la zone de conformité à l’EMT différenciée et la zone de non-conformité, les deux zones étant situées de part et d’autre de la frontière du triangle qui fixe la limite de l’un des paramètres (biais ou écart-type) par rapport à la valeur de l’autre. Il suffit alors de porter le point de coordonnées (Valeur du biais de l’instrument, valeur de l’écart-type résiduel) dans le graphique pour pouvoir statuer sur la conformité. Dans la Figure 6, la zone de conformité est toute la zone située sous le triangle.

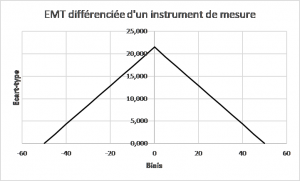
Figure 6 : Représentation d’une EMT différenciée exprimée en ±

Du triangle au prisme

Le propre d’un instrument « mesureur » est de proposer une étendue de mesure. Et le biais, s’il n’est pas corrigé, peut varier en fonction la valeur mesurée (qui se trouve dans l’étendue de mesure, donc entre la valeur minimale mesurable et la valeur maximale mesurable). Pour visualiser la zone de conformité, il convient d’ajouter l’axe de l’étendue de mesure à la Figure 6, comme le montre la Figure 7.

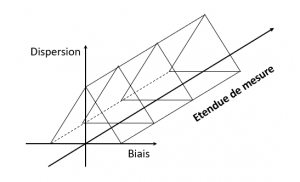
Figure 7 : Zone de conformité en considérant l’étendue de mesure

On peut également imager cette zone de conformité en considérant que l’EMT augmente avec la valeur mesurée (Cas des EMT données en pourcentage de la valeur lue par exemple) pour obtenir la Figure 8.

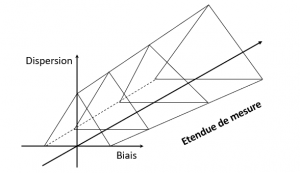
Figure 8 : Cas d’une EMT variable sur l’étendue

Cette forme prismatique rappelle, notamment lorsque l’EMT est constante sur l’étendue, la forme du packaging du Toblerone. Voilà donc une partie du titre dévoilée, passons désormais aux spaghettis …

Du point à l’œuf, puis de l’œuf … aux spaghettis

Dans les Figure 5 et Figure 6, le point de coordonnés (Valeur du biais de l’instrument, valeur de l’écart-type résiduel) qui matérialise les résultats d’un étalonnage est représenté par une étoile

En réalité, cette étoile n’en est pas une. Lors d’un étalonnage, il est possible de déterminer le modèle de l’instrument, la dispersion autour dudit modèle mais aussi, et surtout, les incertitudes sur le modèle et sur la dispersion. Les méthodes de modélisation permettent en effet de calculer des coefficients du modèle et leur matrice de variances/covariances. Et c’est à partir de cette matrice qu’il est possible, en appliquant la loi de propagation du GUM, de calculer l’incertitude sur la correction, c’est-à-dire la barre d’incertitude à associer au biais, en X. On peut alors considérer que l’incertitude en X est de type gaussien, donc symétrique par rapport à la correction.

Il est également possible, en utilisant les propriétés de la loi du Khi Deux, d’estimer l’incertitude sur la dispersion à partir du nombre de degrés de liberté. Cette incertitude donne la barre d’incertitude en Y. Suivant une loi du Khi Deux, cette loi n’est pas symétrique …

Les incertitudes en X et en Y étant ce qu’elles sont, le point se matérialise sur le graphique comme une forme d’œuf (Figure 9), la taille dudit œuf étant fonction du niveau de confiance choisi pour exprimer les incertitudes en X et en Y.

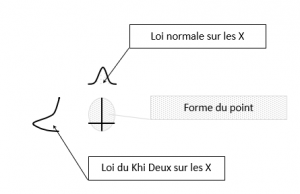
Figure 9 : Forme du point représentant l’instrument

Cette forme se retrouve dans chaque triangle qui parcourt l’étendue de mesure de l’instrument. Si elle ne change pas de taille en Y, elle en change en X du fait de la propagation des incertitudes de modélisation.  Pour la visualiser, on peut simplifier en l’imaginant comme un cylindre, en quelques sortes comme un spaghetti, qui doit rester dans « la boite de Toblerone » pour déclarer la conformité …

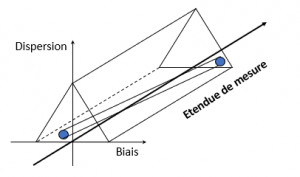
Figure 10 : Instrument Conforme

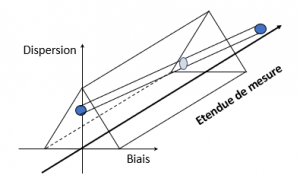
Figure 11 : Instrument non conforme

Conclusion

Cette approche de la vérification de la conformité d’un instrument de mesure offre plusieurs avantages. Elle permet de piloter le risque associé aux mesures en considérant la réalité de l’instrument, c’est-à-dire son effet modélisable et son effet aléatoire qu’elle impose de distinguer. En cela, elle respecte parfaitement la définition du mot « étalonnage » du VIM3 sachant évidemment que toute vérification, au sens du VIM, fait suite à un étalonnage… Elle permet de statuer sur l’intérêt de corriger ou non les valeurs mesurées. En effet, tant que le spaghetti est dans la boite, la correction est inutile. En revanche, s’il en sort, il est possible de voir si une correction permet, ou non, de revenir dans la boite (ie la conformité à l’usage).

Cette méthode permet également d’appliquer sans problème la norme NF ISO/IEC Guide 98-4 en prévoyant une enveloppe supplémentaire de la boite qui est alors, en tridimensionnel, l’équivalent des bandes de garde permettant de piloter le risque global. En utilisant la loi a priori pour déterminer, par des lois a posteriori, la correction à appliquer et la variance des résidus, elle permet aussi de calculer les risques spécifiques.

Il y a une véritable forme d’hypocrisie à se réfugier derrière une « simple vérification » s’appuyant sur des EMT et quelques mesures uniquement. N’y a-t-il pas en effet une forme de prétention presque malsaine à parler d’erreur maximale quand on n’a finalement mesuré que cinq à dix points, parfois moins, d’un instrument qui en compte des milliers ?

Les métrologues ont besoin d’évoluer pour prendre leur place dans le monde 4.0. Jamais le besoin de métrologie, au sens fiabilité des mesures, n’a été aussi important. Au XXème siècle, en collant des étiquettes et en déclarant des conformités comme le fait la métrologie légale, les métrologues industriels et leurs auditeurs se sont trompés (ou ont été trompés ???). Il nous faut réagir, nous en avons les moyens … Le Soleil ne tourne définitivement pas autour de la Terre[9] !

Si la métrologie légale répond parfaitement à ses enjeux (loyauté), les métrologues industriels, eux, passent totalement « à côté de la plaque ». La fonctionnalité n’est pas assurée grâce à eux de nos jours, mais grâce à des exigences beaucoup plus sévères que nécessaire, impactant ainsi la compétitivité (trop cher) et le développement durable (trop gourmand). On peut peut-être continuer à s’amuser comme avant (j’entends déjà tous les conservateurs !) mais l’époque nous offre une véritable opportunité pour changer les choses. L’intelligence artificielle a besoin de données fiables et c’est à nous, métrologues devenus smart, de les lui fournir ! Amis métrologues, votre avenir n’est pas dans les étiquettes et vous avez les moyens de le construire autrement. A vous de jouer !

 

PS : Un énorme merci à mon ami Jean-Marc JUDIC qui, avec l’approche Process Tolerancing qu’il défend avec passion, m’a mis sur la voie des EMT différenciées. Tout comme lui, je considère absolument indispensable de distinguer les effets systématiques et les effets aléatoires tant leur nature et leur impact sont différents. Un grand merci également à mon désormais éternel compagnon Laurent Leblond sans lequel « ma » vision de la métrologie ne serait probablement pas celle-ci …

 

[1] Ce n’est pas tout à fait exact car la métrologie légale procède, en amont de la mise en service des instruments destinés aux échanges commerciaux, à une approbation de modèle, ce qui donne des informations sur la linéarité des technologies mises en œuvre. Cette procédure de validation de modèle n’est pas obligatoire pour les instruments de mesure industriels.

[2] Les incertitudes de mesure sont connues et compatibles avec l’aptitude requise en matière de mesurage (§4.11, de mémoire)

[3] Les métrologues industriels sont en général très ennuyés lorsqu’il n’y a pas de normes qui fixent les EMT alors que, et je ne le redirai jamais assez, les normes sont faites pour ceux qui les écrivent, pas pour ceux qui les lisent et c’est d’ailleurs écrit dessus, en préambule : « La norme est destinée à servir de base dans les relations entre partenaires économiques, scientifiques, techniques et sociaux. La norme par nature est d’application volontaire. Référencée dans un contrat, elle s’impose aux parties. Une réglementation peut rendre d’application obligatoire tout ou partie d’une norme »

[4] Quels sont les points communs entre un fabricant de moules pour l’injection plastique et la société qui utilise ce moule pour fabriquer des pièces injectées lorsqu’il s’agit d’utiliser un micromètre ou un comparateur ?

[5] Je néglige ici, en conscience, la question des incertitudes d’étalonnage pour simplifier le propos

[6] Cf la norme NF ISO/IEC Guide 98-4 et le FD X 07-039

[7] Etalonnage suivant le VIM3 – Application du nouveau concept

http://www.cfmetrologie.com/fr/bibliotheque/etalonnage-suivant-vim-3-detail

[8] Nous retrouvons ici dans une situation finalement très similaire à celle de la MSP (Maitrise statistique des procédés, SPC pour Statistical Process Control en anglais) qui vise à piloter la conformité d’un procédé de fabrication en analysant la dispersion et le décentrage (biais) de sa production

[9] Lire http://www.deltamu.com/fr/Publications/TelechargerArticlePublication/106