Contexte

La mesure n’est pas un besoin en soi pour l’industrie. Elle est un moyen pour tenter d’accéder à la réalité produite. Par exemple, la valeur d’un diamètre (grandeur d’intérêt) ne l’intéresse pas vraiment : ce qu’elle souhaite, c’est savoir si ledit diamètre sera fonctionnel, si l’objet est conforme.

La réponse à cette question passe généralement par la confrontation d’un résultat de mesure à une tolérance, la tolérance étant souvent considérée (à tort en ce qui concerne les tolérances actuelles, à mon avis) comme les limites fonctionnelles minimale et maximale de la caractéristique.

Par ailleurs, il convient d’observer que la mesure intervient bien en amont du constat de conformité d’un objet. La mesure permet en effet, et après la séquence de mise au point (R&D et Méthodes) de piloter et/ou maitriser le processus de production de la grandeur d’intérêt pour tenter d’atteindre le Graal, c’est à dire la conformité.

En général, dans le domaine de la production industrielle, il n’est pas possible de mesurer tous les objets produits pour s’assurer de leur conformité individuelle. Dans ce cadre, on procède donc par prélèvements (échantillonnage) et, à partir des outils développés par les sciences de la Statistique (Inférence), on tente de « deviner » la réalité de la production à partir de quelques unes de ses réalisations (échantillons). Ces techniques sont de nos jours assez répandues et sont connues, généralement, sous le nom de M.S.P (Maitrise Statistiques des Procédés, S.P.C – Statistical Process Control – en anglais).

Il arrive cependant, dans certains domaines spécifiques, que la totalité des « produits ou services » (grandeur d’intérêt) soient vérifiés un à un. C’est le cas, par exemple, des analyses réalisées dans le cadre des laboratoires d’analyse médicale (L.A.B.M), mais aussi pour les parcs d’instruments de mesure dont la gestion fait l’objet de la plus grande attention, pour des raisons essentiellement culturelles, depuis l’avènement des référentiels Qualité, ISO 9000 en tête.

Mesure versus réalité

L’idéal serait de pouvoir accéder à la réalité des objets (ou analyses) produite, c’est à dire la valeur vraie. Or, et tout comme un industriel qui fabrique des écrous vise un nominal qu’il ne saura atteindre, la mesure vise une valeur vraie qu’elle ne pourra atteindre. En effet, une mesure est le fruit d’un processus qui met en œuvre différents facteurs (Objet mesuré, Moyen, Opérateur, Méthode, Environnement) par nature imparfaits, tout comme un process industriel implique lui aussi différents facteurs (Matière, Opérateur, Environnement, Moyen, Usure d’outils, Consignes, …).

De ce fait, et contrairement à une croyance bien ancrée dans notre inconscient collectif depuis maintenant près de 200 ans (1837 : Création de la Métrologie Légale qui est chargée de garantir la loyauté des échanges commerciaux), une mesure ne peut pas être systématiquement juste, tout comme un objet ne peut pas être systématiquement au nominal. Ainsi, il nous faut admettre qu’une valeur mesurée n’est pas la juste représentation de la réalité mais qu’elle contient, en plus, une erreur de mesure, fruit des erreurs individuelles produites par chacun des facteurs du processus de mesure au moment de chaque mesure. De ce fait, la mesure floute et biaise la réalité (Figure 1), ce qui complique une question en apparence simple : mon produit est-il conforme ou encore mon analyse me permet-elle de statuer sur la pathologie du patient ?

On notera que la dispersion apparente est supérieure à la dispersion réelle du fait des erreurs de mesure qui ont l’opportunité de s’exprimer pendant les mesures d’un échantillon. La réalité est donc « meilleure » qu’il n’y paraît. En revanche, la part des erreurs de mesure qui n’ont pas l’opportunité de varier pendant les mesures (et qui se comportent ainsi comme des biais) sont à l’origine de l’écart entre « moyenne apparente » et  « moyenne réelle ». Cet écart joue un rôle négatif car il peut laisser croire que la population est bien positionnée (centrée) alors qu’elle est plus proche qu’il n’y paraît, en réalité, de l’une de ses bornes de tolérance. Ainsi, le taux de « Non Conforme » peut être supérieur, voire significativement supérieur, aux apparences.

Par ailleurs, et dans le cadre d’une production en série, le « mon produit » de la question ci-dessus n’a pas vraiment d’importance puisqu’il s’agit de savoir en réalité si la production, dans son ensemble, est conforme ou pas et pas simplement quelques uns de ses éléments.

Prise en compte des incertitudes de mesure

Il convient, avant toute chose, de remarquer que de nos jours, et malgré 25 ans de certification, les incertitudes de mesure ne sont généralement pas prises en compte dans les décisions. Notre culture nous a laissé croire que les mesures étaient justes et force est de constater que cela ne pénalise apparemment pas la qualité des produits. Rares sont en effet, nous dit-on, les non-conformités fonctionnelles liées à des erreurs de mesure, au sens des incertitudes de mesure. Il peut en effet se produire parfois des erreurs grossières qui n’ont rien à voir avec les problèmes des incertitudes (cf. la sonde partie pour Mars et perdue à cause d’une erreur dans les unités de mesure, les uns pensant en unité anglo-saxonne, les autres en unité métrique).

De ce fait, nous pouvons considérer que les tolérances actuelles, qui servent de base à nos décisions, ne sont pas forcément les tolérances fonctionnelles mais plutôt des limites, déterminées souvent empiriquement, pour valeurs mesurées. Dans cette hypothèse, des mesures de qualité équivalente à la qualité produite historiquement sont suffisantes, au delà de tout autre concept parfois discutable. Autrement dit, tant que CE pied à coulisse mesure comme UN pied à coulisse (ou tout autre type d’instruments évidemment), les choses devraient être acceptables.

Note pour les instruments : Suivant cette hypothèse, il suffit de s’attacher à savoir si un moyen en particulier est différent (ou pas) des autres moyens de sa famille (c’est à dire de son type). Un projet de norme est en cours d’étude pour proposer une méthode qui pourrait permettre de faire ce constat, sur la base de Comparaisons Inter-Instruments (ou C.2.I). La commission Métrologie X07b de l’AFNOR devrait statuer sur le lancement (ou non) du groupe de travail lors de sa prochaine commission plénière, le 11 Février prochain.

Industriellement, il convient donc d’analyser les deux situations évoquées ci-avant :

1. La conformité d’un élément (cas des mesures à 100%, par exemple les analyses médicales)

La nouvelle norme NF ISO/CEI Guide 98-4 éditée en version anglaise en 2013 et traduite en français en 2014 propose une approche très innovante pour définir une stratégie de prise en compte de l’incertitude de mesure dans la déclaration de conformité. Il s’agit désormais de considérer les risques liés à la décision qui se décomposent en :

• Risque Client : Risque de déclarer « Conforme » un « Non Conforme » ou encore Risque de déclarer « Non Malade » un « Malade »

• Risque Fournisseur : Risque de déclarer « Non Conforme » un « Conforme » ou encore déclarer « Malade » un « Non Malade ».

Que ce soit pour le Risque Client ou pour le Risque Fournisseur, la nouvelle norme nous invite à considérer que ces risques ne relèvent pas uniquement des incertitudes de mesure. En effet, il convient également de prendre en compte les risques Process avec un constat simple :  « Livrer » un « Non Conforme » suppose de l’avoir réalisé ! De ce fait, les calculs de risques deviennent vite compliqués et les données d’entrée sont :

• Les incertitudes de mesure (auxquelles l’instrument participe, mais pas seulement lui)
• L’a priori sur le process, c’est à dire la probabilité qu’il produise telle ou telle unité

Sur cette base, la norme définit :

• Le « Risque Spécifique », c’est à dire le risque qu’un échantillon subisse une mauvaise décision (Client ou Fournisseur). L’évaluation de ce risque spécifique impose de réaliser une « révision bayésienne » du résultat de mesure, révision qui permet d’estimer, à partir de l’a priori, de la valeur mesurée et de l’incertitude de mesure, la valeur la plus probable et la distribution des valeurs vraies possibles. C’est à partir de cette révision qu’il est possible de déterminer les risques Client et Fournisseur qui deviennent les critères de décision pour la décision finale.
• Le « Risque global », c’est à dire le taux de « Non Conforme » vu « Conforme (ou « Conforme » vu « Non Conforme ») si TOUTE la production était mesurée, la déclaration de conformité étant établie partir des limites de tolérance. Il est alors possible, si ces risques ne sont pas satisfaisants, soit de revoir le processus de mesure pour atteindre l’objectif, soit de déterminer des bandes de garde qui permettent d’établir de nouvelles limites d’acceptation dans lesquelles les risques sont acceptables (c’est à dire dans les critères fixés). Nous avons eu l’occasion de proposer une stratégie de détermination des bandes de garde basée sur la prise en compte des risques Client et Fournisseur. En effet, ces risques sont souvent assumés finalement par le Client (Car les objets rebutés à tort font partie des coûts de revient, donc des prix de vente, desdits objets) et des bandes de garde permettant de minimiser la somme pondérée des risques Client et Fournisseur est probablement une approche industriellement pertinente (lire article « ISO 98-4 : Incertitude de mesure et déclaration de conformité »)

Note pour les instruments : Dans le cas où il est nécessaire de diminuer l’incertitude de mesure pour diminuer les risques et atteindre les objectifs, l’analyse du processus de mesure permet de déterminer les facteurs les plus influents, donc ceux sur lesquels il convient d’agir, dans la mesure du possible. L’E.M.T des instruments peut alors être définie à partir des calculs de risques et du poids que l’instrument peut atteindre dans le processus de mesure. Il n’y a donc aucune règle d’or qui peut fonctionner car les risques sont liés à chaque production, donc à chaque entreprise. Il est ici important de souligner qu’un instrument maitrisé est évidemment une condition nécessaire à une mesure de qualité, mais surement pas une condition suffisante. Tout le processus de mesure doit être considéré, et en particulier les causes les plus importantes que l’intuition (ou les croyances) ne suffit pas à identifier.

2. La conformité d’une production (cas de la mesure dans le cadre de la M.S.P notamment)

La M.S.P repose sur des bases statistiques éprouvées. Il s’agit de déterminer les paramètres (Moyenne et écart-type) d’une production supposée suivre une loi de probabilité normale (on pourrait étendre cette technique à tout type de lois) et de s’assurer que ladite production ne dépasse un taux fixé de « Non conforme ». Cette « assurance » est établie à partir de paramètres calculés (moyenne, écart-type) et des tolérances à réaliser. Ces paramètres (Cp et Cpk par exemple) sont réévalués périodiquement et des cartes de contrôle sont établies pour s’assurer du maintien de la performance du process. La limite contractuelle du paramètre Cpk permet d’établir le taux de « Non conforme » accepté par le client.

L’évaluation des paramètres Cp et Cpk repose sur des valeurs mesurées d’échantillons de la production. Or, la mesure introduit des erreurs, certaines ayant un caractère aléatoire au cours des mesures de l’échantillon (Erreurs HO, telle que la répétabilité – EV – par exemple), d’autres non (Erreurs LO, telle que la reproductibilité Opérateur – AV – par exemple. En effet, si l’opérateur ne change pas lors des mesures, l’erreur qu’il amène dans le processus reste « constante » dans toutes les mesures). On peut également considérer, comme cause d’erreurs LO, l’instrument de mesure utilisé lors de la mesure d’un échantillon (car il est rare d’en changer entre les mesures, tout comme il est rare de changer l’opérateur). Cette participation aux erreurs LO contribue au décalage entre « réalité » et « apparence », donc à la différence entre le taux de « Non Conforme » apparent et le taux réel.

Dans les règles de la MSP, et afin de ne pas être trop perturbé par les erreurs de mesure dans l’analyse des données, le concept de « capabilité des processus de mesure» a été développé. Il s’agit de faire en sorte que les erreurs de mesure soient négligeables pendant les mesures de façon à ce que les paramètres Cp et Cpk apparents soient très proches de la réalité du process. L’étalonnage/vérification des instruments de mesure semble suffire, aux yeux des créateurs de la méthode, pour négliger leurs contributions aux erreurs de mesure lors des études (un instrument déclaré « Conforme » est considéré « négligeable », ce qui est fort discutable !).

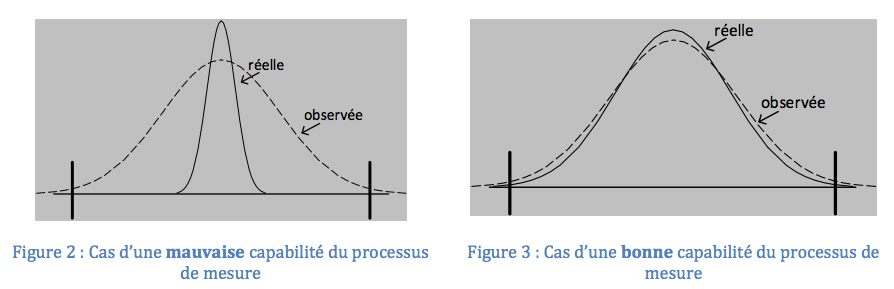
Ainsi, le concept de « capabilité d’un processus de mesure » vise à s’assurer que le processus de mesure pourra évaluer les Cp, Cpk d’un Process qui, eux, permettent de déterminer le taux de « Non Conforme » réellement produit. La « capabilité d’un processus de mesure » ne permet pas de garantir la pertinence d’une décision quant à la conformité d’un objet particulier (ou d’une analyse) à une spécification, contrairement à ce que de plus en plus de personnes semblent penser … (Lire l’article « Qu’est ce que la capabilité ? »)

Dans le cas des figures précédentes, on constate qu’une bonne capabilité du processus de mesure ne garantit pas à elle seule le risque. Il est sans doute préférable d’être dans la situation figure 2 avec une mauvaise capabilité car la réalité crée peu de « Non Conforme », contrairement au cas décrit par la figure 3 (avec une très bonne « capabilité » mais beaucoup de « non conforme » généré par le process)

Perspectives

A bien y réfléchir, les données disponibles lors d’une étude R&R, enrichies par les prélèvements périodiques réalisés dans le cadre du suivi d’un process, peuvent permettre de donner un encadrement du taux de « Non Conforme », ce qui est le plus souvent le besoin industriel dans une relation saine Client-Fournisseur, sur la base de quelques réflexions simples :

1 : Les objets prélevés dans la production pour l’étude R&R permettent d’évaluer une première estimation des paramètres de la production. Ces estimations sont entachées d’incertitude que la statistique sait évaluer (Loi de Student, pour la moyenne, et loi du Khi Deux pour la variance)

2 : Les répétitions de mesures par différents opérateurs permettent d’évaluer une partie des incertitudes de mesure (Liée aux opérateurs, dans l’application stricte du R&R).Là encore, la statistique permet d’évaluer l’incertitude sur les paramètres EV (répétabilité) et AV (Fidélité intermédiaire liée à la différence entre les opérateurs). Il est toujours possible d’améliorer la connaissance de l’incertitude de mesure totale en réalisant d’autres types d’expériences (Par exemple un R&R en changeant d’instrument, au lieu de changer l’opérateur, ce qui revient à évaluer la fidélité intermédiaire « inter-instruments ». Les C.2.I évoquées plus haut permettent, contrairement aux simples étalonnages, d’évaluer ce paramètre pour une famille d’instruments) ou en ajoutant des incertitudes évaluées par une méthode de type B (Cf le G.U.M), par exemple l’impact de l’environnement.

3 : En tenant compte des incertitudes sur l’évaluation de tous ces paramètres (Moyenne et dispersion de la production, erreurs LO et HO dues au processus de mesure) et de leur composition (Observé = Réalité + Mesure donc Réalité = Observé – Mesure !), il est possible, sur la base des résultats expérimentaux, d’encadrer le taux de « Non Conforme » produit réellement par le process.

4 : En se « nourrissant » des informations obtenues lors des prélèvements périodiques, et sous réserve qu’ils confirment que l’échantillon en cours d’analyse n’est pas différent, au sens statistique, de ce que nous connaissions antérieurement du process (connaissance construite à partir des prélèvements précédents), il est possible d’améliorer la connaissance des paramètres (Moyenne et dispersion de la production, erreurs LO et HO dues au processus de mesure), donc d’améliorer la connaissance de l’encadrement du taux de « Non Conforme » produit.

5 : Dans cet esprit, le « constat d’un état » (actuel) est transformé en « Gestion de la connaissance ». Il intègre en plus les propriétés singulières des mesures (Erreurs de type LO – Low Opportunity de varier dans l ‘échantillon – et de type HO – High Opportunity de varier dans l’échantillon), ce qui permet de les optimiser (C’est à dire d’agir sur les causes qui ont un effet négatif réel, plutôt que de s’intéresser aux seuls instruments de mesure tel que la Métrologie Légale depuis 200 ans). Ce cadre permet de déterminer les limites d’acceptation (EMT) des instruments de mesure. Il dépasse largement le concept de capabilité qui ne dit finalement rien des risques Client et Fournisseur. Une telle stratégie répond donc parfaitement aux objectifs de la relation Client/Fournisseurs : La maitrise d’un taux de « Non Conforme » accepté et l’adaptation des moyens pour y parvenir, dans un esprit du « juste nécessaire ». 

Connaître la réalité : une problématique quasi-universelle

Finalement, la problématique de connaître la réalité au travers de mesures est le quotidien du métrologue. Que ce soit, comme évoqué précédemment, la maitrise d’un process de production (MSP), d’un équipement spécifique (Enceinte climatique, four de traitement, …) ou encore les performances d’une famille d’instruments de mesure (C.2.I), il s’agit toujours de déduire de mesures une réalité sous-jacente. Cette recherche se fait au travers de données échantillonnées (il n’est pas possible de mesurer toutes pièces d’une production, tout comme il n’est pas possible de mesurer tous les « points » d’un volume d’une enceinte climatique) entachées d’incertitudes liées aux mesures.

Fort de ce constat d’une problématique quasi-universelle, une conférence dans le cadre du prochain Congrès International de Métrologie (CIM 2015) a été proposée pour donner les modèles, les stratégies de mesure et les formules permettant d’estimer l’encadrement du taux de « Non Conforme » généré réellement par le process et, le cas échéant, les stratégies pour diminuer l’impact « incertitude de mesure » dans cet encadrement (Répétition des mesures, changement de moyens de mesure, optimisation des « gestes opérateurs », …).

En attendant, je vous souhaite de bonnes fêtes de fin d’année …