Bien choisir sa périodicité d’étalonnage est l’une des tâches demandées au métrologue. Dans un précédent article, nous avons discuté des stratégies proposées par la  FD X07-014 et l’ILAC-G24 / OIML D 10. Dans le présent article, je traite de l’approche d’un autre document, le RP-1 [1] « Establishment and Adjustment of Calibration Intervals » du NCSLI [2]. C’est un document très complet (161 pages) qui reprend le problème à la racine et propose des solutions à partir d’une approche mathématique rigoureuse basée sur les données historiques des précédents résultats d’étalonnage. Mon but n’est pas ici de résumer le document, mais plutôt de présenter mon interprétation de sa vision de la problématique et des éléments qui me paraissent intéressant à retenir.

Quel risque couvre l’étalonnage ?

Le document commence par se poser la question essentielle. Pourquoi étalonner de manière périodique ? Il propose ensuite une modélisation de la problématique en posant quelques définitions et hypothèses qui méritent que l’on s’y attarde. À partir de là, il liste différentes stratégies possibles de choix de périodicité. Enfin il en détaille l’application, de la plus simple à la plus complexe.

Selon le RP-1, l’exigence première est que le produit final fabriqué soit conforme à ses exigences. L’état de conformité du moyen de mesure introduit donc un risque sur cette déclaration de conformité du produit fini. Mais l’étalonnage périodique n’est pas, à priori, une opération qui permet de prévenir les non conformités. Le but de l’étalonnage est de limiter l’utilisation d’un moyen hors tolérance à un niveau acceptable. Ce niveau acceptable est défini en fonction du risque accepté sur le produit fini. Dans le monde industriel, ce niveau de risque est majoritairement défini en fonction du coût que peut engendrer un mauvais produit fini (mauvaise fiabilité ou non-conformité). Donc le choix de la périodicité est directement lié à un coût. De manière pragmatique, le RP-1 rappelle aussi qu’on étalonne de manière périodique essentiellement parce que c’est demandé par les normes, mais ça ne change pas la raison profonde de la périodicité d’étalonnage.

§ 1.4 Many diverse calibrations interval-analysis and management systems have emerged over the past few decades. This is due in no small part to requirements and recommendation set forth in … The above requirements stem from the fact that a prime objective is that attributes of products fabricated … will be fielded in an acceptable condition

Cette introduction sur les raisons de la périodicité me parait remettre en quelques sortes « les pendules à l’heure ». La première question à se poser pour définir une « bonne » périodicité d’étalonnage est donc de savoir pourquoi on la cherche. Il n’existe pas de périodicité universelle qui serait bonne. Chaque entreprise a ses propres contraintes et objectifs, il est donc normal que les périodicités soient liées à ce que fait l’entreprise. L’autre aspect souligné par ce document est l’aspect financier. L’étalonnage coûte cher. Il sert à réduire un risque, donc un coût que pourrait engendrer une non conformité. Il est donc justifié que le coût d’étalonnage, au sens large (coût brut d’étalonnage, coût de gestion, coût d’immobilisation, …) soit un paramètre important à prendre en compte dans le choix de la périodicité.

L’étalonnage, garantie du passé

Cependant, je ne suis pas tout à fait d’accord avec cette vision du RP-1 sur l’intérêt de la périodicité. L’étalonnage sert bien à garantir la traçabilité des mesures. Il sert aussi de référent quand un doute survient sur un processus de mesure. Mais la contrainte périodique de l’étalonnage imposée par les normes sert, de mon point de vu, principalement à rassurer. L’étalonnage garantit le passé et ne présume aucunement du comportement du moyen dans son utilisation future. Le RP-1 le souligne en disant que l’étalonnage périodique ne peut pas prévenir une non-conformité d’arriver, mais il s’assure plutôt que la situation, lorsqu’elle survient, ne dure pas.

§1.3 the principal goal … of calibration interval analysis … is limiting the usage of out-of-tolerance attributes to an acceptable level

Or dans les faits, dans le monde industriel, la périodicité d’étalonnage n’intervient pas directement dans le risque de non conformité du produit fini. Et heureusement, étant données les périodicités que l’on peut rencontrer (6 mois, 1 an, 2 ans, 5 ans, …), car cela ferait prendre des risques beaucoup trop importants. Que se passe-t-il lorsqu’un moyen est découvert non conforme suite à un étalonnage périodique ? On s’empresse généralement de faire une dérogation qui justifie que cela n’a pas d’impact sur le produit fini. En effet l’industriel a mis en place de nombreuses stratégies pour garantir la fiabilité de sa production bien avant que l’étalonnage périodique ne lui soit imposé. Et il s’appuie toujours sur ces stratégies qui ont fait leurs preuves par le passé. La version 2015 de l’ISO 9001 peut d’ailleurs être interprétée dans ce sens. La notion d’étalonnage périodique du moyen n’intervient que dans le paragraphe « 7.1.5.2 Traçabilité » précédé de la phrase « Lorsque la traçabilité de la mesure est une exigence ou… un élément essentiel visant à donner confiance… l’équipement de mesure doit être: … » : n’est-ce qu’une histoire de confiance et d’exigence qui n’a pas de rapport direct avec la réalité de la fiabilité de la production ? En effet, ce qui doit être surveillé et maintenu c’est le processus de mesure dans son ensemble. C’est ce qui est exigé dans le paragraphe précédent §7.1.5.1 de l’ISO 9001.

Mais revenons à l’étude du document.

Introduction de la fiabilité d’un moyen

Une fois la raison de la périodicité d’étalonnage bien définie, le RP-1 modélise la problématique en posant les hypothèses et les définitions suivantes. La connaissance sur la valeur d’une caractéristique étalonnée diminue avec le temps. Cette diminution de connaissance est appelée « croissance de l’incertitude » (au sens du « doute sur ») dans le temps. Ce doute atteint un « niveau inacceptable » au bout d’un certain temps et une opération d’étalonnage devient alors nécessaire. Un niveau inacceptable de doute correspond à une probabilité de non-conformité du moyen pouvant avoir une incidence importante sur le produit.

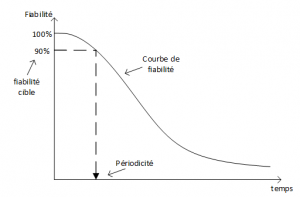
Pour modéliser cette idée,  le RP-1 introduit la notion clé de fiabilité du moyen. C’est une fonction qui décrit l’état de conformité au sens statistique) du moyen dans le temps. Il s’agit de la probabilité qu’a un moyen d’être conforme à la suite d’un étalonnage à une date t. C’est la clé de voûte de la modélisation du RP-1. En effet, si l’on connait la courbe de fiabilité d’un moyen et que l’on est capable de définir une fiabilité cible acceptable, la périodicité d’étalonnage en découle.

L’intérêt de la notion de fiabilité est qu’elle est applicable à tout type de situation : moyen qui dérive, moyen qui ne dérive pas mais qui subit des chocs aléatoires, moyen qui vieillit, etc… La forme de la courbe de fiabilité s’adaptera à la nature des phénomènes qui entraîne la non-conformité du moyen.

Confusion entre incertitude et fiabilité

Cette modélisation de la problématique ne me convainc pas complètement. En effet, l’hypothèse de base de la « croissance de l’incertitude » me parait mal définie. Le terme incertitude est utilisé dans deux sens différents dans le document, ce qui amène une certaine confusion dans la compréhension. Dans le glossaire, l’incertitude de mesure est définie avec le sens classique en métrologie « paramètre associé à un résultat de mesure qui caractérise la dispersion de la valeur du mesurande ». Mais dans le document, elle représente plutôt le doute, quantifiée par la fiabilité, c’est à dire la probabilité d’être non-conforme. Ce flou de langage, incertitude « doute » sur l’état du moyen  et incertitude « métrologie », n’aide pas à comprendre le principe.

Prenons un exemple pour exprimer la confusion des termes. L’incertitude de mesure au pied à coulisse (pàc) a été estimée pour un processus donné à 50 µm pour un parc donné de pàc. Suite à une étude sur l’étalonnage périodique annuel du parc, on constate que 2% des pàc présentent un biais significatif, c’est-à-dire un problème de justesse. Il est alors envisagé de prendre en compte ce biais dans l’estimation d’incertitude. Effectivement, le risque d’avoir un pied à coulisse présentant un biais augmente l’incertitude sur le résultat de mesure fait avec un pàc, sachant que ladite incertitude concerne sans distinction tous les pàc (biaisés ou non). Si j’ai peu de chance d’avoir un pàc biaisé, l’incertitude ne sera pas beaucoup impactée. Si au contraire, la quasi-totalité des pàc finissent par présenter le biais au moment de l’étalonnage périodique, l’incertitude sera impactée de la totalité du biais constaté. Pour le dire autrement, plus j’ai de pàc qui présentent le biais, moins j’ai confiance dans les résultats obtenus avec ce type de moyen, donc plus mon incertitude est grande. C’est ce que j’ai appelé plus haut « l’incertitude doute », qui dépend, comme son nom l’indique, du doute que j’ai sur la fiabilité de mon moyen.
Mais attention, l’incertitude est augmentée pour l’année entière, et pour tous les pàc, elle ne varie pas progressivement au cours des 12 mois. C’est cette incertitude fixe, pour un périmètre donné, que j’ai appelé l’incertitude « métrologique ». Elle sera fixe et dépendra de la stratégie d’étalonnage, elle n’a pas pour objectif de pouvoir augmenter avec le temps. Dès la première utilisation après l’étalonnage, l’incertitude initiale de 50µm est augmentée pour toute la durée de validité du moyen, car l’évènement qui cause les biais peut arriver au bout de 3 jours, 3 mois, ou pas.
Donc l’incertitude « métrologique » n’augmente pas avec le temps, elle est fixe sur la période définie. C’est elle que l’on utilise pour prendre des décisions par rapport à un résultat de mesure.
L’incertitude « doute » n’est pas l’incertitude que l’on utilise habituellement, elle est définie par le RP 1 pour quantifier la variation de l’incertitude « métrologique » quand on fait varier un des paramètres de l’estimation, la périodicité d’étalonnage. Le RP-1 recherche la périodicité optimale pour que l’incertitude « métrologique » (fixe pour toute la durée d’utilisation) reste acceptable pour le besoin.
Le lecteur comprendra dès lors qu’affirmer que « l’incertitude augmente avec le temps » peut prêter à confusion.

Des hypothèses contradictoires ?

Je trouve très intéressante leur manière de clairement identifier leurs hypothèses. Cela permet de définir le besoin et aussi dans quel cas le besoin n’existe pas, c’est-à-dire que l’étalonnage périodique n’a pas de sens. On peut déjà identifier deux cas que l’on trouve souvent dans le monde industriel. Si la non-conformité est immédiatement identifiable lors de l’utilisation (grâce à une surveillance), l’étalonnage périodique n’a pas de sens (§5.4.5). Si les performances métrologiques du moyen sont surdimensionnées par rapport au besoin, l’étalonnage périodique peut être jugé inutile (§3.10.2.1). Ces deux cas sont clairement énoncés dans le document.

Cependant, il y a tout de même 2 hypothèses qui me semblent contradictoires dans le modèle.

1- la non-conformité du moyen n’est détectable qu’en étalonnage et non pas en utilisation.
Si en utilisation, le problème sur le moyen est immédiatement détecté (par l’utilisateur, une dérive du processus, une non fonctionnalité immédiate du produit …), l’étalonnage périodique n’a plus de sens (chapitre 7, point 4).
2- la part du moyen doit être significative dans l’incertitude du processus de mesure.
Le RP-1 recherche le moment où l’incertitude de mesure est trop importante par rapport à la prise de décision par rapport à une tolérance. Si la part d’incertitude du moyen est négligeable, elle n’impactera jamais la décision. C’est ce qu’il exprime dans le §3.10.2.1

Donc la part du moyen doit être prépondérante dans l’incertitude de mesure du processus, mais la non-conformité n’est détectable qu’en étalonnage et non pas en utilisation (par l’opérateur par exemple). Ce cas me semble très rare car les processus de mesure sont très souvent surveillés, soit explicitement par exemple par le passage d’une pièce de référence, soit implicitement par exemple par le fait qu’on mesure une valeur attendue et qu’on peut être alerté lorsqu’on n’obtient pas la valeur habituelle. Cette surveillance est censée alerter sur un écart inacceptable du processus de mesure (sinon elle n’a pas de sens), et donc du moyen puisqu’il est censé être l’élément majoritaire de l’incertitude.

Une modélisation précise du problème

La modélisation de la fiabilité me semble également intéressante. C’est un modèle qui ne prend pas comme hypothèse que l’instrument dérive, ce qui est rarement le cas contrairement aux idées reçues (principalement à cause d’une mauvaise utilisation du terme « dérive »). Pourtant, il tient bien compte du comportement du moyen suivant l’historique des étalonnages. Je prendrais là encore l’exemple des pieds à coulisse. Les pieds à coulisse ne dérivent pas (cf. Étude statistique de la dérive du pied à coulisse, CIM 2015 [3]) ils tombent, se déforment, … Une non-conformité de pàc détectée en étalonnage n’est certainement pas due à une usure progressive d’un composant du moyen ou à l’âge du pàc, mais plutôt à un évènement ponctuel ou accidentel. Comment, dans ce cas, définir la bonne périodicité ! L’idée de la méthode est dans un premier temps d’identifier quel est le taux de pàc non conformes sur la durée d’étalonnage historique. Il s’agit ensuite d’adapter la périodicité en fonction de la fiabilité choisie. Par exemple, si, sur un historique d’étalonnage annuel, le métrologue constate que 98% des pàc sont conformes et qu’une fiabilité de 90% serait suffisante, il peut élargir l’intervalle de périodicité pour atteindre la fiabilité de 90%. Cependant choisir un niveau de  fiabilité et en déduire un intervalle n’est pas forcément une opération simple et le problème est développé plus loin dans le document. Mais l’idée est intéressante car elle est compréhensible et pleine de bon sens. Elle fait intervenir la notion de risque et le résultat dépend du besoin de chaque entreprise. Si la mise en œuvre n’était pas si complexe, je plébisciterais cette méthode pour de nombreux cas.

Proposition de stratégies

Suite à cette introduction, le RP-1 revient sur les différents types de méthodes de choix de périodicité qu’il classe en 6 catégories dans le chapitre 4. Il donne les avantages et inconvénients de chacune d’elle et n’en rejette complètement aucune :

1- Intervalle général pour tous les équipements
Méthode facile à mettre en place, mais elle ne peut pas réellement répondre au besoin. Elle est sans doute très couteuse car elle obéit à la périodicité du moyen le plus exigeant.
2- Intervalle emprunté
Utilisation d’intervalles définis par un organisme externe (constructeur du moyen, Laboratoire d’étalonnage, …). Cette méthode se révèle souvent peu en cohérence avec l’utilisation du moyen où le risque n’est en général pas connu ou pas pris en compte par l’organisme externe.
3- Analyse technique
Les données disponibles lors de l’analyse technique sont rarement liées à la périodicité d’étalonnage, sauf peut-être les recommandations du constructeur. Elles sont plus associées à des performances métrologiques et permettent donc par exemple d’identifier les EMT de manière pertinente. Mais la fiabilité réelle du moyen et son comportement dans le temps sont souvent empiriques, associés à des évènements ponctuels non nécessairement représentatifs. Au final la périodicité choisie est souvent arbitraire et plus faible que nécessaire.
4- Méthode Réactive
Utilisation du dernier résultat d’étalonnage pour ajuster la périodicité. Méthode non conseillée car trop dépendante du seul dernier résultat d’étalonnage, donc fortement entachée de l’incertitude d’étalonnage.
(§2.6.4.1 : Methode A1 is not recommended bu remains documented in this RP to discourage its « reinvention » and maintain awarness of the drawbackw of similar methods)
5- Estimation de la fiabilité
Utilise l’historique d’étalonnage pour définir la périodicité. Méthode très efficace mais complexe à mettre en place.
6- Autres méthodes
Il existe de nombreuses autres méthodes, qui ne rentrent pas dans les catégories précédentes qu’il n’est pas possible d’analyser qu’au cas par cas.

Les méthodes 1 à 4 sont décrites comme étant peu efficaces. Néanmoins, le RP1 ne les rejette pas totalement en mettant en avant une problématique de coût. Mais c’est bien évidemment la méthode 5 qu’il préconise.

Les méthodes statistiques

Le RP1 explique ensuite comment mettre en place les méthodes 4 et surtout 5.
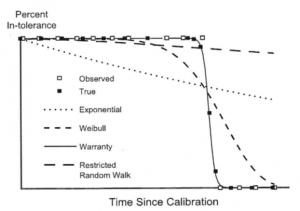
Dans un premier temps, il faut avoir une source de données fiables, clairement définies et relativement importantes. La courbe de fiabilité, élément essentiel de la méthode, est déduite de ces données. Le RP1 nous guide en proposant différentes modélisations de fiabilité en fonction du comportement du moyen : moyen qui s’use progressivement ou qui présente des défauts aléatoires ou qui a une durée de vie limitée, etc…

Un traitement mathématique rigoureux et complexe est proposé pour chacune des méthodes.

La partie traitement mathématique n’est pas triviale, ni à comprendre, ni à mettre en œuvre. Le RP1 propose des méthodes de plus en plus complexes, mais même la première méthode n’est pas simple à mettre en œuvre. Il en a bien conscience et il met naturellement en garde sur le coût de mise en place et de maintenance de la méthode. Il estime cependant que le bilan est en général positif.
Le point positif de ce document est son approche très structurée de la problématique en essayant d’analyser et d’identifier les différents aspects du problème. De plus les méthodes mathématiques proposées sont intéressantes (bien que complexes à mettre en œuvre comme indiqué plus haut), notamment la modélisation de la fiabilité et des courbes proposées.

Les limites du document

Les périodicités proposées pour l’application numérique semblent un peu étranges. Elles sont très faibles (45 jours pour le premier exemple, optimisé à 47! §B.3.1 et 3 semaines pour l’exemple § D.6). Or, les périodicités traditionnelles dans les industries sont plutôt de l’ordre de l’année.
L’autre élément pouvant être jugé douteux tient dans les exemples de budgets de mise en œuvre de la méthode qui sont chiffrés de l’ordre de 100k$ à 2M$ (§4.7 point 3). Le RP1 annonce qu’ils peuvent être amortis en 1, voire 2 ans. Amortir, c’est-à-dire « économiser », en 1 an jusque 2M€ d’étude initial suppose des budgets d’étalonnages très élevés, donc très loin des budgets moyens que nous rencontrons classiquement.
On peut regretter que les méthodes proposées ne se basent que sur un aspect binaire de la problématique : la conformité ou non du moyen. Aucune méthode proposée ne tient compte du résultat numérique de l’étalonnage. Cela peut paraître dommage de ne pas avoir à tenir compte de cette information pourtant coûteuse…

Pour finir, je pense que le RP1 a été conçu par des automaticiens. Il semble très orienté « maintenance » des processus complexes de production. La problématique n’est pas la même pour l’étalonnage. L’étalonnage n’est pas une maintenance préventive, il n’a pas pour but de maintenir la conformité du processus de mesure. L’industriel a mis en place pour cela des systèmes de surveillance bien plus efficaces car souvent quasi instantanés dans leur capacité de détection. À partir de ce constat, la notion de fiabilité n’a pas tout à fait le même impact que pour la maintenance. L’étalonnage est une opération qui permet de faire un état des lieux du moyen, état de lieux souvent dé-corrélé des problématiques de production. Les impacts financiers sont aussi d’un autre ordre. Une machine de production qui tombe en panne implique un arrêt de production, donc nécessairement une perte (plus ou moins importante) immédiatement quantifiable. Un moyen de mesure non conforme ne signifie pas que la production est mauvaise, mais juste qu’on ne l’a pas suivie efficacement. Dans la réalité, on s’empresse souvent de rédiger une dérogation pour finalement justifier du non impact sur la production passée. L’analyse n’est pas du tout la même.
Si le processus de mesure est vraiment à risque, l’industriel mettra en place des surveillances capables de détecter les problèmes, il ne s’appuiera pas uniquement sur l’étalonnage. Donc la vraie problématique n’est pas la périodicité d’étalonnage, mais bel et bien la mise en place de surveillances efficaces. Et le RP1 ne traite pas suffisamment des problématiques de surveillance.

Conclusion

Dans cette vision des choses, la mise en place des procédures proposées dans le RP1 semble surdimensionnée par rapport au risque et au besoin et donc au final inapplicable. Je dirais même que l’analyse du besoin proposé en début de document écarte quasiment tous les équipements du besoin d’étalonnage périodique. Cependant, l’idée de fiabilité et le traitement rigoureux qui est fait de ce concept, restent très intéressants mais pour des applications très particulières (et pas nécessaire pour l’étalonnage) car l’investissement pour l’étude est très important.

GLOSSAIRE

[1] Recommended Practice – (RP-1) : Establishment and Adjustment of Calibration Intervals – 2010 – NCSLI
[2] NCSL International (NCSLI) (« National Conference of Standards Laboratories ») – http://www.ncsli.org/
[3] Étude statistique de la dérive du pied à coulisse – 17ième Congrès international de métrologie (CIM), Christophe Dubois