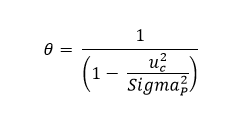Le JCGM a publié, en 2012, le document JCGM 106 traitant de la prise en compte des incertitudes de mesure dans la déclaration de conformité. Ce document a été quasiment immédiatement repris sous forme de norme ISO qui, elle-même, vient d’être reprise dans la collection française sous la référence NF ISO CEI Guide 98-4.

De mon coté, je n’ai pas été surpris par cette norme (en tout cas dans un premier temps) car cela fait plus de dix ans que je défends l’approche « Risque Client » plutôt que l’approche « Capabilité » qui a été sortie de contexte, comme j’ai pu l’écrire récemment pour la revue Contrôles Essais Mesures.

Ainsi, la définition de » bandes de garde » pour maintenir un « Risque Client » malgré une incertitude de mesure trop importante ne m’est pas du tout étrangère, bien au contraire. J’ai écrit de nombreux articles sur ce thème. J’ai même présenté, avec Dimitri VAISSIÈRE, une conférence dans le cadre du Congrès International de Métrologie de Lille, en 2007.

En avançant dans la réflexion sur le sujet des bandes de garde, j’ai pu récemment soulever la question du « Risque Fournisseur ». En effet, si les bandes de garde peuvent permettre de maitriser le Risque Client, elles présentent l’inconvénient de faire augmenter corrélativement, et considérablement, le Risque Fournisseur. Or, que ce soit dans le cadre des vérifications métrologiques (Gestion d’un parc d’instruments) ou dans le cas général du contrôle de produits, le Risque Fournisseur finit toujours par être payé par le client final. En effet, il faut bien que quelqu’un assume l’impact financier des mauvaises décisions qui grèvent, d’une façon ou d’une autre, le coût des produits conformes. De ce fait, j’ai eu l’occasion de présenter une stratégie « Bande de garde » qui respecte la nouvelle norme mais aussi les enjeux financiers : une bande de garde qui permet d’optimiser la somme pondérée des risques Client et Fournisseur. Je présenterai, en partenariat avec M. Laurent LEBLOND (P.S.A), une conférence sur ce sujet dans le cadre du prochain Congrès Africain de Métrologie, à Pretoria, début Avril 2014. Deltamu met à disposition une application gratuite sur Excel pour faire les calculs, par simulation numérique.

Mais voilà… La vraie surprise de cette norme est ailleurs : le Risque Spécifique !

La stratégie des bandes de garde concerne la vérification de la totalité des objets d’un lot. Les risques déterminés représentent le taux d’objets qui ont fait l’objet d’une mauvaise décision (dans un sens ou dans un autre). Le produit de ces taux par le nombre d’individus dans le lot donne le nombre d’objets concernés par les mauvaises décisions, sans pouvoir, évidemment, les identifier.

La norme définit également le concept de Risque Spécifique. Il s’agit là de déterminer, pour un objet en particulier, le risque de mauvaise décision. Habituellement, ce risque est déterminé par la surface de la gaussienne qui, soit dépasse des tolérances quand la valeur mesurée est vue « conforme », soit à l’intérieur de la tolérance quand elle est vue « non conforme ». Ainsi, et dans cette représentation, la valeur mesurée et l’incertitude associée sont les deux seuls paramètres considérés, la valeur mesurée étant alors représentée (donc considérée) comme la valeur la plus probable… Or, et nous l’avons tous vécu, nous savons qu’il existe d’autres informations que nous considérons habituellement « intuitivement ». Qui, en effet, n’a jamais remis en cause une mesure parce qu’elle lui paraissait incohérente ? Et comment ce sentiment d’incohérence survient-il ?

Cette perception de l’incohérence provient simplement d’une attente « a priori ». En effet, lorsqu’on étalonne par exemple un capteur de température, on sait bien « quelque part » qu’on ne risque pas de trouver des erreurs supérieures à… ce que l’habitude nous a appris. Chaque métrologue, dans son contexte industriel, a en effet un « a priori » sur ce qu’il mesure, « a priori » souvent non formalisé, mais bien présent. Tous les métrologues sont donc déjà, sans le savoir, des « bayésiens ». Ainsi, la mesure n’est pas réellement « une découverte » (en tout cas rarement) mais la confirmation, ou l’infirmation, d’une valeur attendue. Cette vision est bel et bien celle mise en avant dans la nouvelle norme NF ISO CEI Guide 98-4 !

Fort de cette remarque, il est aisé de se convaincre que la mesure n’est pas la seule information disponible pour prendre une décision. Il est aussi possible de considérer l’information « a priori » concernant le process qui a réalisé l’objet mesuré. La mesure et son incertitude deviennent alors une information supplémentaire qui va permettre de réviser « l’a priori » pour conduire à une connaissance « a posteriori ». Cette loi dite « a posteriori » représente la synthèse de toute l’information disponible. Elle permet de définir, à partir de l’a priori (process) et de la nouvelle information (mesure), la distribution des valeurs vraies de l’objet mesuré et de définir ainsi les risques de mauvaises décisions.

Lorsque le process suit une loi normale (de moyenne P et d’écart-type Sigma_P) et que la mesure suit elle aussi une loi normale d’écart-type u_C, les paramètres (Moyenne « Mu » et écart-type « Sigma ») de la loi « a posteriori » sont donnés par les formules suivantes :
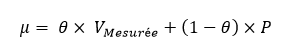
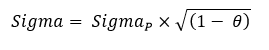Avec :

Cette évolution est absolument fondamentale. En « digérant » cette nouvelle vision, le métrologue pourra enfin apporter toute sa valeur à l’entreprise en sortant du modèle déterministe « Valeur mesurée = Valeur la plus probable » couteux en mauvaises décisions. Une fois convaincu que les décisions doivent prendre en compte la connaissance « a priori », il faudra « construire la connaissance » cet « a priori », c’est à dire mettre la métrologie au service des process et plus uniquement, comme c’est trop souvent le cas, au service du contrôle. Chaque mesure que produit l’entreprise devient, dans ce contexte, une information supplémentaire qui permet d’améliorer la connaissance de ses process, donc à améliorer ses décisions… Les 3 évolutions de la connaissance, schématisées ci-dessous par la visualisation des lois « a priori », « mesure » et « a posteriori », pour une même mesure et une même incertitude de mesure permet d’entrevoir toute la richesse de cette approche.

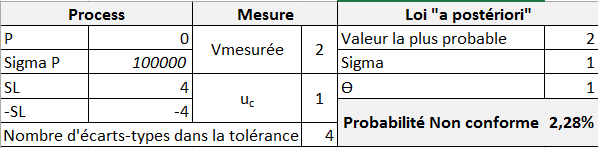
Situation N°1 (A priori inconnu) :

Valeur mesurée : 2
Incertitude type u_C : 1

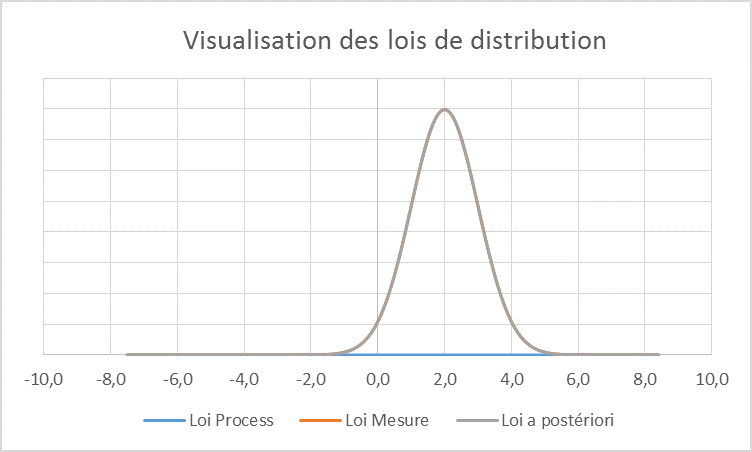Dans ce cas, seule la mesure donne de l’information et la probabilité (dans le niveau actuel de connaissance) que l’objet mesuré soit « non conforme » est calculée à 2,28% (Le sigma_P est fixé à 100000. Ce paramétrage permet de « simuler » aucun « a priori » sur le process)

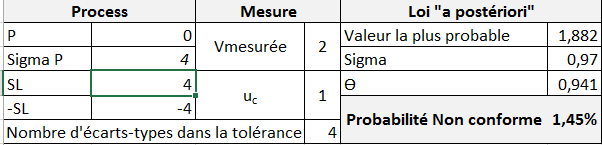
Situation N°2 (On commence à accumuler de la connaissance, l’A priori n’est plus tout à fait inconnu) :

Valeur mesurée : 2
Incertitude type u_C : 1

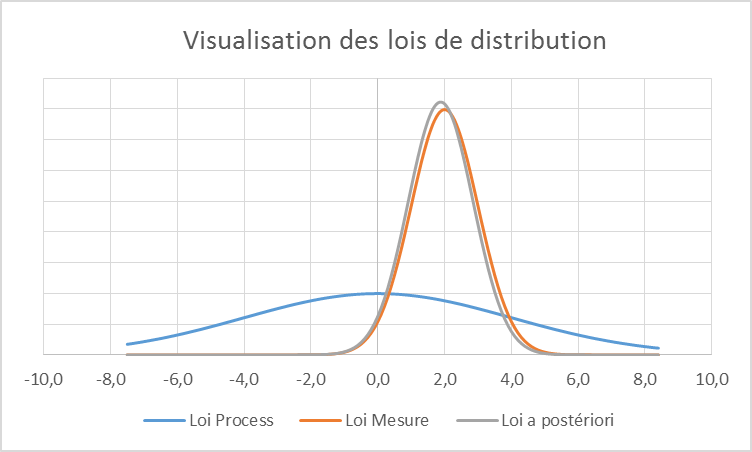On remarque ici que la valeur la plus probable commence à se décaler vers la moyenne du process (ce sera toujours le cas). La connaissance « a posteriori » s’améliore et le risque de « non conformité » diminue :

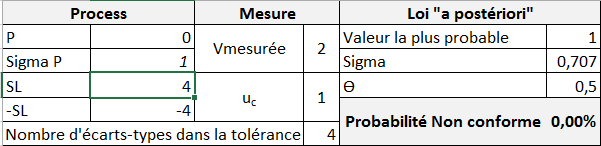
Situation N°3 (La connaissance sur le Process est acquise) :

Valeur mesurée : 2
Incertitude type u_C : 1
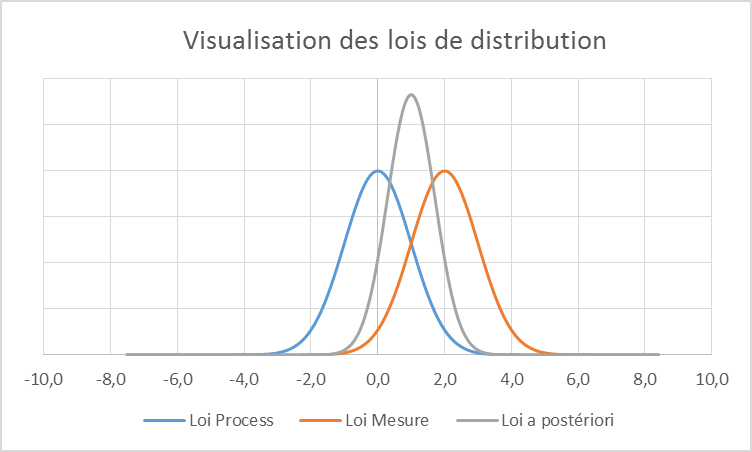On « mesure » bien ici tout l’intérêt de connaitre le process pour prendre de bonnes décisions. Avec la même qualité de mesure (incertitude) que dans le cas N°1, le risque de mauvaise décision est devenu quasi nul du fait de la prise en compte du process, puisque connu…

Conclusion

Comment être plus démonstratif ? Que faudrait-il faire ou dire de plus pour convaincre tous les métrologues que cette norme est l’outil le plus puissant que nous n’ayons jamais eu à notre disposition pour faire progresser le métier ?
De mon coté, je me réjouis de cette norme, de ses principes et de l(a)’ (r)évolution qu’elle engendre. La métrologie peut, et doit enfin, devenir l’outil de la connaissance… connaissance des process, connaissance des risques et seule la connaissance permet de progresser. Il ne reste plus qu’à !!!!