Il est d’usage d’analyser un processus d’étalonnage en établissant un bilan d’incertitude, c’est à dire
en listant toutes, ou du moins le plus grand nombre, de causes d’incertitude. Cette analyse peut être
effectuée à l’aide de la méthode dite des 5 M.

Le bilan des causes d’incertitudes consiste à identifier les différentes composantes d’incertitudes.
Elles sont ensuite présentée dans un tableau et chaque composante est ensuite quantifiée, à l’aide
d’une méthode de type A ou de type B (cf. GUM). Les différentes composantes sont exprimées à
l’aide d’incertitude type ou de leur carré. Il s’agit alors de variances.

Pour les évaluations de type B, on examine, pour chaque composante, l’étendue des variations
probables et on attribue à chacune une loi de distribution. Au cours de cet exercice, on exprimera donc
les variations maximales de chaque effet. Dans cette analyse, nous tentons d’établir un bilan
représentatif de ce qui se passe tout au cours du temps. Ce bilan peut être remis en cause
périodiquement, notamment lors du réétalonnage des étalons. En effet, nous ne souhaitons pas
refaire une évaluation d’incertitude à chaque étalonnage. Le tableau ci-dessous présente un exemple
d’évaluation d’incertitude pour un étalonnage en métrologie dimensionnelle par une méthode de
comparaison mécanique.

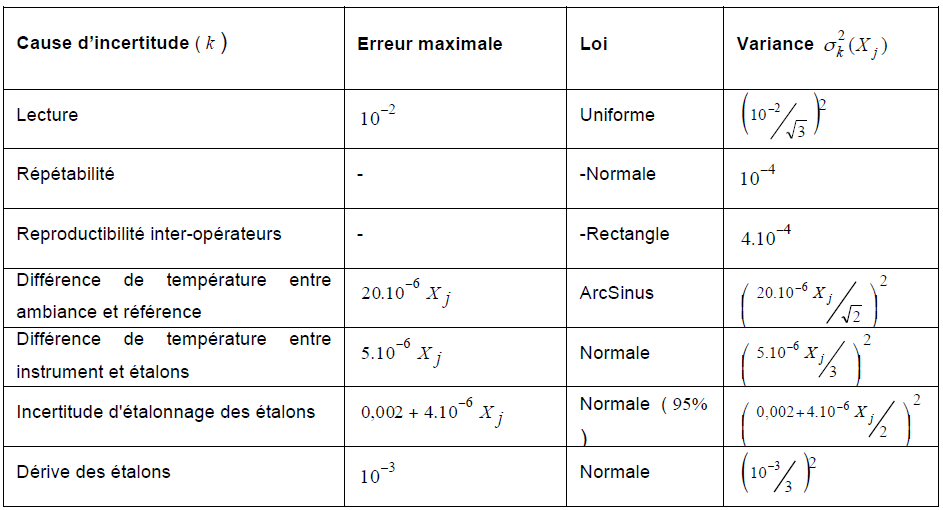Figure 1 : Tableau d’incertitudes classique

Or, la réalisation d’un étalonnage ne dure pas, en général, très longtemps. Aussi, certains effets
variables sur du long terme ne le sont pas pendant le temps de l’étalonnage et se comportent alors
comme des erreurs systématiques qu’il ne faudrait pas attribuer par l’erreur systématique de
l’instrument en cours d’étalonnage. Il convient donc d’étendre l’analyse des causes d’incertitude de
mesure à ce phénomène en se demandant si, pendant le temps de la mesure (l’étalonnage), elles ont
ou non la possibilité, l’opportunité, de s’exprimer (c’est à dire de varier).

Par exemple, la répétabilité peut être assimilée à une erreur aléatoire qui peut prendre
des valeurs différentes à chaque mesure (par définition, la répétabilité représente la dispersion des
mesures qui sont réalisées en un bref moment, par le même opérateur, avec le même moyen).
Suivant ce constat, ce facteur s’exprime différemment à chaque mesure. Pour qualifier ce fait, on
parlera de cause d’incertitude HO, pour « High Opportunity » … de varier pendant les mesures.

La température, pour une mesure dimensionnelle, induit elle aussi une erreur aléatoire mais il est aisé
de constater que ce n’est pas un effet « HO ». En effet, si, dans chaque bilan des causes
d’incertitude, le métrologue cherche à quantifier la dispersion maximale que peut prendre la
température dans son laboratoire pour estimer l’impact maximum que peut produire la température
(quel que soit le moment où se produit la mesure, pourvu que ce soit dans ce laboratoire), il est
entendu que ladite température ne varie pas beaucoup, entre deux mesures successives, dans l’ensemble de ses valeurs possibles. En fait, pendant le temps de l’étalonnage (quelques minutes, voire dizaines de minutes), la température ne variera tout au plus que dans un pourcentage donné de sa plage de variation maximale. Par exemple, imaginons que nous procédions à l’étalonnage d’un instrument insensible à la température (règle en invar par exemple) par comparaison aux indications d’un banc de mesure doté d’une règle en acier. Si la température du laboratoire est, au moment de l’étalonnage, à 21°C plutôt qu’à 20°C (température de référence en métrologie dimensionnelle), la règle du banc va se dilater alors que le moyen étalonné reste invariant. Cette dilation du banc de mesure va générer des écarts avec la règle, écarts qui n’ont rien à voir avec des erreurs dues à la règle mais à la température du laboratoire. Aussi, l’observation ne correspond pas à une erreur de l’instrument étalonné : il ne doit donc pas être corrigé. Il en est de même si pendant le temps de l’étalonnage, la température varie aléatoirement sur quelques pourcents de son étendue possible : l’écart observé ne relève toujours pas de l’instrument étalonné lui-même. Nous parlerons alors d’un caractère « LO» (Low Opportunity) pour qualifier les erreurs aléatoires dues à de tels facteurs.

Aussi, un modèle d’étalonnage où les incertitudes sur les étalons sont négligeables et prenant en
compte les erreurs liées aux effets LO (δ L(X j )) et les erreurs liées aux HO (ε j ) peut s’écrire :

∀j∈<1…J > Yj = b₀ +b₁X_j +δ_L(X_j ) +ε_j(X_j )

avec :

δ_L(X_j ) ~ Normale(0; σ_LO(X_j))

ε_j(X_j) ~ Normale(0; σ_HO(X_j)) indépendantes et les (ε_j(X_j)) j ∈<1…J > indépendantes.

Pour quantifier σ_HO²(X_j) (dite variance HO») et σ_LO²(X_j) (dite variance « LO»), il suffit d’ajouter le
caractère LO ou HO dans un bilan des K causes d’incertitude et de l’exprimer par un pourcentage.

La part de variance LO pour chaque facteur k considéré, facteur auquel est associé une variance
σ²_k(X_j). Ce coefficient, noté Lk, prend donc conventionnellement la valeur 0% lorsque la variance
considérée est totalement «HO» puis augmente jusqu’à 100% pour les causes strictement invariables
pendant le temps des mesures. Les facteurs étant considérés comme indépendants, la variance
« HO» (respectivement « LO») du processus d’étalonnage est alors la somme pondérée des
variances « HO » (respectivement « LO») des causes d’incertitude :

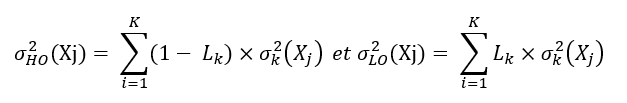Par exemple, pour la température ci-dessus, ce coefficient serait de 80% si l’on estime que la
température peut varier de 20% de la plage totale pendant le temps des mesures. Pour un effet de
reproductibilité inter-opérateur et si l’opérateur ne change pas tout au long d’un étalonnage, le
coefficient serait alors de 100%.

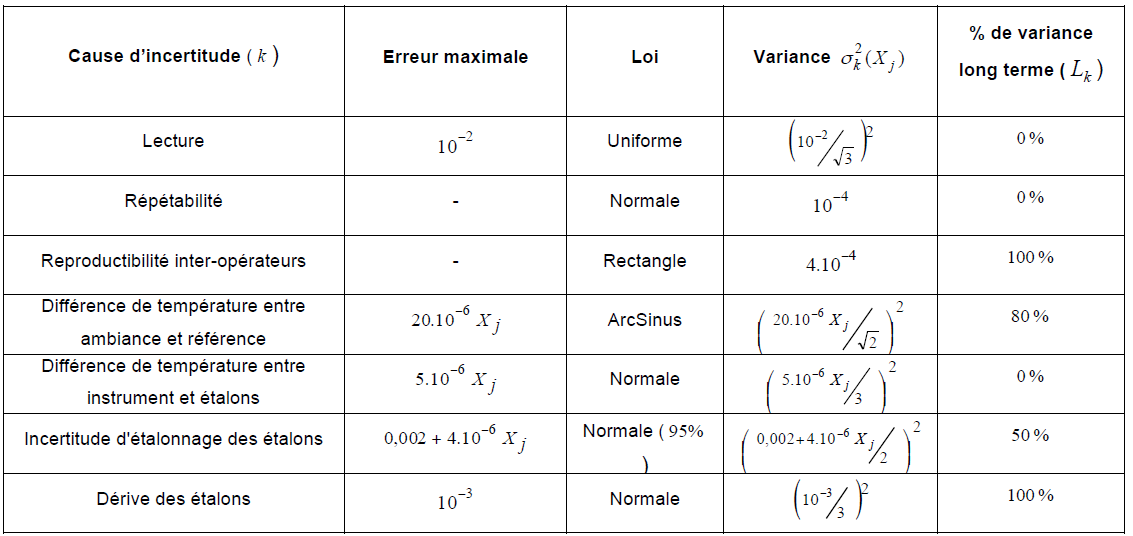Figure 2 – Exemple de prise en compte du caractère « LO» ou « HO» des causes d’incertitude

Evidemment, ces coefficients ne sont que des estimations dont la qualité dépend de l’analyse du
métrologue. Il s’agit de prendre en compte de façon physique le phénomène de « l’effet LO» qui
perturbe l’évaluation de l’erreur systématique de l’instrument en « se faisant passer pour elle ».

Par exemple, un modèle d’étalonnage où l’erreur propre de l’instrument, en chaque point étalonné, s’additionne à une erreur δ_LO propre aux conditions spécifiques de l’étalonnage (eu égard à la part LO des facteurs d’incertitude) et à une erreur ε_j, réalisation de la part HO des causes d’incertitude d’étalonnage, peut s’écrire :

∀j∈<1…J > Yj = b₀ +b₁X_j +δ_LO +ε_j

Ce modèle permet de structurer une matrice de variances/covariances des erreurs aléatoires d’un modèle d’étalonnage linaire direct à étalons indépendants :

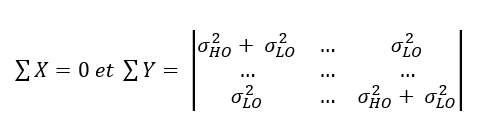
Dans cet exemple, on considère qu’il n’y a pas d’incertitude sur les étalons (les X) et que l’incertitude est constante sur chacun des points d’étalonnage, la réalité est évidemment plus complexe …