Chez Deltamu, nous nous sommes engagés à répondre à chacune des questions posées lors du webinar #11 : « Simulation numérique : un outil universel à l’usage des métrologues », qui a eu lieu jeudi 25 février à 10H30. Vous trouverez dans cet article l’ensemble des questions qui ont été posées via le chat et auxquelles nous n’avons pas pu répondre en live. Nous restons à votre disposition par mail pour toute autre précision ou pour obtenir les supports de présentation.

Simulation numérique : un outil universel à l’usage des métrologues

Questions/Réponses

Question : Comment peut-on vérifier si une loi suit une distribution normale ?

Réponse : Les phénomènes observés dans la nature tendent vers une loi normale. Le « théorème central limite » en donne l’explication/justification mathématique. Cependant, il faut bien comprendre que l’hypothèse de normalité n’est qu’une modélisation pratique de la réalité. Vos données ne suivent pas une loi normale ! Déjà rien que par le fait qu’elles sont bornées par la capacité de votre équipement de mesure et que vos données sont discrétisées par la résolution de votre équipement. Donc lorsqu’on souhaite vérifier la normalité d’une distribution, il faut déjà se poser la question de la qualité de notre modèle. Quelle est la qualité de nos estimateurs (moyenne, écart type), jusqu’où a-t-on besoin d’utiliser cette hypothèse de normalité (pour voir des ppm ?). Si on y regarde de « trop près », l’hypothèse de normalité sera sans doute à un moment réfutée.

Une approche empirique par l’outil graphique (superposition de l’histogramme des valeurs à une courbe de loi normale, boite à moustache, droite de Henry, etc.)  est déjà une solution qui vous donnera une première idée de votre normalité. Cela peut être suffisant.

Vous pouvez ensuite vous orienter vers des outils mathématiques plus objectifs : test de Shapiro-Wilk,  Test du Khi Deux (ou D’Agostino), test d’Anderson-Darling, … Nous ne détaillerons pas ici les détails des calculs pour réaliser ces tests.

Attention à l’interprétation faite des résultats de ces tests. En réalité, le test ne vous garantit pas la normalité, il vous dit si votre jeu de données est incompatible avec l’hypothèse de normalité.  En conséquence, si vous faite un test de normalité avec très peu de données (une vingtaine par exemple), il y a de grandes chances qu’il ne détecte pas de non normalité étant donnée la faible quantité d’information. Cela ne veut pourtant pas dire que votre phénomène est distribué selon une loi normale, mais plutôt que l’hypothèse n’est pas absurde.

D’un autre côté, si vous effectuez le test avec énormément de données (plusieurs milliers), il se peut que le test ne passe pas. En effet, il faut se rappeler que les phénomènes observés tendent vers une loi normale, mais souvent ne sont pas exactement de loi normale. Et donc si vous avez énormément d’informations, le moindre écart à la normalité est immédiatement détecté.

Moralité, comme toujours, les outils statistiques vous donnent des informations, mais c’est l’interprétation de l’utilisateur de ces outils qui doit s’exercer.

Question : À partir de quel seuil on peut estimer que 2 variables sont corrélées ?

Réponse : La notion de corrélation est continue de 0 à 100%. Il n’y a pas de seuil de corrélation ou non. Dans la pratique tout dépend de votre cas de figure.
Si vous avez peu de données, la qualité de vos estimateurs est faible et l’estimation de la corrélation est mauvaise. Dans ce cas, pour dire qu’il y a corrélation entre deux paramètres, on attend effectivement une forte valeur (80% par exemple). Cependant, elle pourra difficilement être utilisée numériquement.
Si vos données sont nombreuses, une corrélation de 20% peut être détectée.

Question : Il faut déjà une connaissance a priori de la corrélation ? Comment l’estimer ?

Réponse : Dans le cas de calcul d’incertitude, on part effectivement du principe que la corrélation est identifiée par la compétence métier et on ne cherche à quantifier la corrélation que pour les cas identifiés. Dans le cas plus général de suivi de données de plusieurs paramètres, au contraire, on cherche à identifier les corrélations que la compétence métier n’aurait pas immédiatement détectées. On l’estime à partir de données récoltées grâces aux outils mathématiques de covariance ou corrélation. Des outils plus évolués de data-scientistes peuvent aussi mettre en évidence des corrélations.  Il faut également être attentif à la qualité de l’horodatage des données, si de multiples mesures sont prises simultanément. De plus, les données récoltées sont des données mesurées, donc « floutées » par rapport à la réalité. Il peut donc arriver qu’une corrélation entre deux paramètres ne soit pas identifiée à cause de l’incertitude de mesure. Il est donc important d’avoir des données « propres » avant de faire un traitement.

Question : Comment s’assurer que la distribution est celle d’une loi normale ? Est-ce que le graphique suffit ?

Réponse : Tout dépend de ce que l’on veut faire. Un graphique peut suffire. Voir la question 1.

Question : Je n’ai pas compris comment sont déterminés les coefficients de la matrice de covariance ?

Réponse : Les coefficients de la matrice de variance/covariance peuvent être déterminés de 2 manières :

• Une estimation à partir de sa compétence métier peut permettre d’estimer le facteur de corrélation. Par exemple si 2 paramètres sont totalement liés, la corrélation est estimée à 1. On peut prendre par exemple le cas deux paramètres liés à la température, qui seraient dans le même environnement, donc qui « verraient » la même température. À partir de la variance et de la corrélation, on peut en déduire la covariance : covariance(a,b) = corrélation(a,b)*s_a*s_b
• Une estimation expérimentale de la covariance entre 2 paramètres. Estimation mathématique de la covariance entre 2 paramètres dont les données sont issues d’une expérience ou d’un suivi de production (formule cov() sous Excel par exemple).

Question : La transposée d’une matrice ne change-t-elle pas le sens physique d’une matrice ?

Réponse :  La transposée change simplement l’ordre dans lequel les valeurs sont présentées. Elle ne change pas les valeurs. Les données en ligne sont représentées en colonnes et inversement.

Exemple :

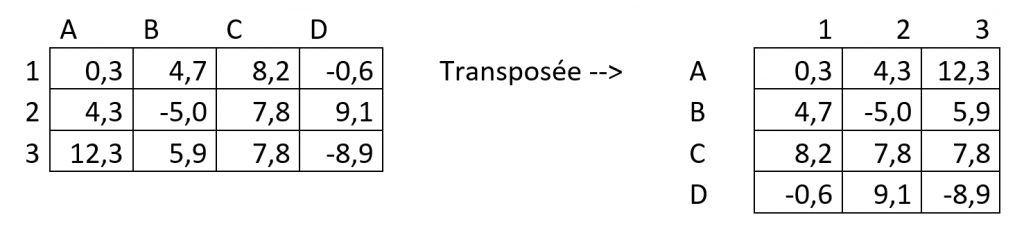
Dans cette exemple la cellule B3 (ou 3B) garde la même valeur 5,9 et le même sens physique. Elle est simplement localisée différemment dans le tableau.

Question : Est-ce que l’épaisseur du tube est intégrée dans la variable masse ?

Réponse : Dans l’exemple pédagogique du webinar, les paramètres suivis de la production de tubes sont uniquement :

• Masse ;
• Hauteur ;
• Rayon interne.

L’objectif est de montrer le sens « physique » de la covariance : il y a un lien entre la hauteur et la masse, mais aussi entre le rayon interne et la masse.

Question : Si on connait Cov M/L et cov M/R peut-on en déduire cov R/L ?

Réponse : La covariance traite des liens 2 à 2 entre les paramètres. Cependant, ces liens 2 à 2 ne sont pas totalement indépendants les uns par rapport aux autres. On comprend bien que dans notre cas à 3 paramètres M, L et R,  si M/L sont liés à 100% et M/R sont liés à 100%, alors R/L sont nécessairement liés à 100%. Il y a donc effectivement des liens entre les covariances, on ne peut pas avoir n’importe quoi. Ce lien dépends du nombre de paramètres et de leur valeur. Dans notre cas à 3 paramètres M, L et R, si on connait cov(M,L) et cov(M,R), on ne peut pas nécessairement en déduire cov(R,L) mais on a tout de même des restrictions sur les valeurs possibles. Par ailleurs, toutes les corrélations ne sont pas linéaires, ça complique encore les choses pour déterminer la 3^ème à partir des 2 premières …

La vidéo intégrale du webinar est disponible sur 

Vous ne voulez rien manquer de notre actualité ? Suivez-nous sur Linkedin et/ou inscrivez-vous à notre Newsletter !