Nous nous sommes engagés à répondre à chacune des questions posées lors du séminaire web #1 : « Les outils fondamentaux de statistiques au service de la métrologie », qui a eu lieu mercredi 15 Avril dernier à 10H. Vous trouverez dans cet article l’ensemble des questions qui ont été posées via le chat et auxquelles nous n’avons pas pu répondre en live.  Nous restons à votre disposition par mail pour obtenir le support de présentation ou pour toute autre précision.

« Les outils fondamentaux de statistiques au service de la métrologie »

Questions/Réponses

Question : Est ce qu’il vaut mieux utiliser une carte MSP aux écarts types plutôt qu’aux étendues ?

Réponse : Même si nous ne sommes pas des spécialistes de la MSP, je pense qu’il est préférable d’utiliser des écarts-types plutôt que des étendues d’échantillons, comme nous l’avons vu à la fin du webinar. L’étendue est beaucoup trop sensible à l’échantillonnage et l’écart-type sert justement à voir plus loin que l’étendue, à « deviner » ce que nous n’avons pas vu dans l’échantillon et qui existe pourtant !

 

Question : Comment procéder à l’évaluation de l’écart type, si on n’a pas une loi normale ?

Réponse : La formule de l’écart-type est indépendante de la loi parente. Lorsque nous disposons d’une série de valeurs numériques, l’écart-type se calcule toujours par la même formule et nous déconseillons fortement d’utiliser de vieilles méthodes basées sur l’étendue de l’échantillon. En revanche, lorsque nous ne disposons pas de valeurs, on estime l’écart-type à partir de l’étendue du phénomène (présumée ou connue) et de sa loi de probabilité (présumée ou connue). On parle alors d’une évaluation de type B, évaluation très sensible aux hypothèses formulées quant à l’étendue et à la loi lorsque ces deux paramètres ne sont que présumés …

 

Question : Est-ce qu’on peut parler d’estimateur de l’incertitude type et quel est son nom ?

Réponse : Nous pouvons commencer par dire que l’incertitude est de toute façon toujours une estimation, nous ne pourrons jamais la connaitre parfaitement. En fait, il semblerait que les membres du groupe qui a rédigé le GUM (Guide pour l’expression des incertitudes de mesure) aient introduit la notion d’incertitude-type pour les évaluations d’écart-type par une méthode de type B (c’est-à-dire à partir de l’étendue et de la loi de probabilité du phénomène). Il semble en effet difficile de comparer un estimateur d’écart-type obtenu avec un échantillon de valeurs (approche purement statistique) et un autre estimé à partir d’une étendue (approche plus empirique) et c’est pourquoi on a donné un nom différent. On parle ensuite « d’incertitude type composée » lorsque, après avoir fait la somme de toutes les variances du processus de mesure, on en extrait la racine carrée. On multiplie ensuite cette incertitude type composée par un facteur d’élargissement, noté k, qui permet de choisir un niveau de confiance pour définir un intervalle de confiance. On parle alors d’incertitude élargie. Par convention, les laboratoires utilisent k=2 qui conduit à un niveau de confiance e 95% (en considérant que l’incertitude de mesure suit une loi normale).

 

Question : Même si notre échantillon est faible, cela peut dégrader la qualité de l’estimateur de l’écart type.

Réponse : La qualité de l’estimateur de l’espérance mathématique (moyenne) ou d’écart-type est évidemment directement dépendante du nombre de valeurs dont nous disposons pour les calculer. Les lois de Student (pour la moyenne) et du Khi Deux (pour l’écart-type) permettent de calculer les intervalles de confiance des paramètres, au niveau de confiance choisi (Cf ci-dessous).

 

Question : Pourquoi l’incertitude augmente lorsqu’on augmente le facteur d’élargissement k ?

Réponse : En fait, cette question permet d’introduire celle de la définition même du mot « incertitude de mesure ». La définition du VIM n’est pas très éclairante et une définition plus claire pourrait être, par exemple : « Loi de probabilité des erreurs de mesure ». Cette définition est parfaitement univoque puisqu’elle n’induit rien sur la forme de la loi (elle peut être gaussienne ou autre), ni sur la position (elle peut être biaisée ou pas). Avec cette définition, la notion de facteur d’élargissement deviendrait inutile puisque, notamment dans le cas gaussien, l’incertitude de mesure serait entièrement définie par une moyenne (un biais devant être corrigé en théorie) et un écart-type. Mais comme on a choisi d’évoquer, pour l’incertitude de mesure, des intervalles de confiance, ils sont bien évidemment d’autant plus grands que le niveau de confiance est élevé.

 

Question : ECARTYPE.STANDARD ou écartype moyen dans Excel, lequel choisir ?

Réponse : Il existe la fonction ECART.MOYEN() qui calcule la moyenne des valeurs absolues des écarts à la moyenne d’une série. Cet outil a de mauvaises propriétés mathématiques (non dérivable en zéro) et n’est pas très utilisé.

Excel propose 4 formules d’écarts types :

ECARTYPEP et ECARTYPE.PEARSON sont identiques, mais la première est obsolète pour Excel (le nom a sans doute été jugé pas assez univoque). Elles permettent de calculer l’écart type d’une population complète, finie.

ECARTYPE ou ECARTYPE.STANDARD sont identiques, mais la première est obsolète pour Excel (là aussi, un nom a sans doute été jugé imprécis). Elles permettent de calculer un estimateur d’écart type à partir d’un échantillon de la population. Dans la pratique en métrologie, on se retrouve dans ce cas et c’est donc l’une de ces 2 fonctions qu’il faut utiliser.

 

Question : Comment savoir la loi de probabilité pour les erreurs de mesure que j’ai au labo de métrologie ?

Réponse : Dans la plupart des cas, on considère, comme le GUM, que les facteurs à l’origine de l’incertitude sont suffisamment nombreux et indépendants pour que leur résultante, l’incertitude, soit gaussienne. Il est possible, lorsqu’on a su répertorié toutes les causes d’incertitude et leur loi de probabilité respective, de connaitre la loi de probabilité par simulation numérique (Simulation de Monté Carlo). Il est alors possible de prendre en compte les éventuelles covariances entre les causes d’incertitude …

 

Question : Valeurs aberrantes par GRUBBS ou COCHRAN.

Réponse : Cette question est très pertinente et justifierait de longs développements. Nous réfléchissons à organiser un webinar sur ce thème. La détection d’éventuelles valeurs aberrantes dans un échantillon est une étape indispensable avant de calculer les estimateurs. Beaucoup de tests sont disponibles dans la littérature pour faire ce travail de détection. Il faut également s’assurer que les données de la série sont bien indépendantes entre elles et là encore, il existe des tests. Désolé de ne pas pouvoir développer plus ici …

 

Question : Quelle loi prendre en fonction du paramètre (main d’œuvre, méthode, milieu, …). Est-ce que c’est spécifié dans le GUM ?

Réponse : Cette question est au cœur des évaluations de type B (cf. ci-dessus) et c’est l’une des plus compliquées dans le cadre de l’évaluation des incertitudes de mesure. En fait, on utilise souvent 3 lois (j’écarte en conscience la loi triangle) : la loi normale, la loi uniforme et la loi en dérivée d’arc-sinus. En fait, il faut donc se demander si le phénomène que j’analyse à autant de chance de produire chacune des valeurs possibles entre les bornes de son étendue (et dans ce cas il est considéré uniforme), s’il produit plus de valeurs au milieu de l’intervalle (il est alors considéré gaussien) ou si les valeurs qu’il produit sont plus souvent proches des bornes (et on part dans ce cas sur une loi arc-sinus). C’est vraiment au métrologue de se déterminer …

 

Question : Est-ce que je peux mélanger des unités différentes pour estimer l’incertitude de mesure. Par exemple lorsque j’ai un essai de flexion.

Réponse : Non, surtout pas, ça n’aurait aucun sens. Le cas que vous décrivez se réfère à ce que nous appelons, chez Deltamu, un modèle d’intérêt pour le distinguer d’un modèle de mesure directe, c’est-à-dire le cas dans lequel on mesure directement la grandeur d’intérêt. La situation des modèles d’intérêt est donc celle dans laquelle vous ne mesurez pas directement ce qui vous intéresse (la résistance en flexion) mais des grandeurs qui permettent de la calculer. Vous avez évidemment des incertitudes sur les grandeurs d’entrée mesurées (probablement un effort et une flexion dans votre cas) et ces incertitudes se propagent via l’équation mathématique qui les relie à la grandeur d’intérêt. C’est à partir de cette équation qu’il est possible, soit de calculer les dérivées partielles de chaque grandeur mesurée et d’appliquer la loi de propagation du GUM, soit de simuler des valeurs possibles pour les grandeurs d’entrée et de calculer à chaque simulation la grandeur d’intérêt (Simulation numérique de Monte Carlo), pour déterminer l’incertitude sur la grandeur d’intérêt.

 

Question : Vous avez cité la loi de Student. Quelle est son utilisation, son utilité ?

Réponse : La loi de Student est la loi de probabilité complexe, nous ne rentrerons pas dans les détails de sa construction ici (cf. https://fr.wikipedia.org/wiki/Loi_de_Student ). Ses propriétés permettent de définir un intervalle de confiance contenant  (espérance mathématique de la population parente) sachant les  valeurs de l’échantillon, donc la moyenne  et l’estimateur d’écart-type , la variance de la population parente étant ici inconnue. La largeur de cet intervalle de confiance dépend évidemment du niveau de confiance souhaité (Voir question suivante « Pourriez-vous rappeler le lien entre lois Student / khi2 et valeurs moyennes/écart-type ».

 

Question : Comment justifier d’être en présence d’une loi normale ?

Réponse : Voir question : « Comment savoir la loi de probabilité pour les erreurs de mesure que j’ai au labo de métrologie ? »

 

Question : Pourriez-vous rappeler le lien entre lois Student / khi2 et valeurs moyennes/écart-type ?

Réponse : Cf question « Vous avez cité la loi de Student. Quelle est son utilisation, son utilité ? ». Pour aller plus loin que dans la réponse précédente, nous pouvons préciser comment calculer les bornes de l’intervalle de confiance à l’aide d’un tableur :

Figure 1 : Extrait du fascicule « Quelques outils de la Statistique pour la métrologie » édité prochainement par Deltamu

Il est plus compliqué d’expliquer la nature de la loi du Khi Deux. Elle décrit la loi de probabilité de la somme des carrés de  réalisations de lois normales centrées réduites (autrement dit,  degrés de liberté).  A partir des propriétés de cette loi de probabilité, il est possible d’établir un intervalle, au niveau de confiance choisi, contenant  lorsqu’on dispose d’un échantillon de  valeurs à partir duquel on peut calculer . Il est aisé de calculer les bornes de l’intervalle de confiance à l’aide des tableurs :

Figure 2 : Extrait du fascicule « Quelques outils de la Statistique pour la métrologie » édité prochainement par Deltamu

 

Question : Quelle est la différence entre loi normale et loi normale centrée réduite ?

Réponse : On parle d’une loi normale centrée réduite lorsqu’on considère une loi normale, de moyenne égale à 0 et d’écart-type égal à 1. On évoque aussi la « normalisation d’une série de données » lorsqu’on transforme les données initiales en loi centrée réduite. Cette transformation se fait simplement en calculant la moyenne et l’écart type de la série initiale et en calculant, pour chaque valeur de la série initiale, son « écart normalisé » par la formule :

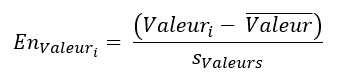
Note : La normalisation des données n’impose pas le fait que la loi parente soit gaussienne. Elle marche dans tous les cas. On parle donc, plus généralement, de loi centrée réduite.

 

Question : Quelle est grandeur statistique qui permet d’estimer la reproductibilité de mesure ?

Réponse : La reproductibilité est une dispersion dans des conditions particulières (voir définition du VIM). Elle est de ce fait estimée par un écart-type. Il convient néanmoins de préciser ce que recouvre la « reproductibilité ». Le VIM comme l’ISO 5725-1 précisent que cet écart-type est obtenu dans des conditions de reproductibilité qu’il faut donc préciser. Est-ce que tous les facteurs potentiels de variabilité ont varié pendant les mesures ou est-ce qu’on a choisi de n’en faire varier que quelques-uns. On parle alors de fidélité intermédiaire, ou de reproductibilité inter-quelque chose. Lorsque tous les facteurs ont varié (cas général des essais interlaboratoires), la reproductibilité peut représenter la part aléatoire de l’incertitude de mesure.

 

Question : L’observation des phénomènes aléatoires permettent donc de définir également l’incertitude de type B?

Réponse : Ce ne sont pas les incertitudes qui sont de type B ou de type A, mais leur méthode d’évaluation. Pour une évaluation de Type A, on dispose de valeurs et pour une méthode de Type B, on dispose de l’étendue et de la forme de la loi de probabilité du phénomène.

 

Question : En métrologie industrielle, quel est le nombre de mesures nécessaire afin déterminer la reproductibilité de mesure ?

Réponse : La reproductibilité est déterminée à partir d’un d’écart type. À partir du nombre de mesures vous pouvez déterminer un intervalle de confiance de la reproductibilité. En fonction de votre besoin de précision (donc de la largeur de l’intervalle) et du coût de réalisation des mesures, vous pouvez déterminer un nombre de mesures optimum qui vous convient. En général, on effectue une série de mesures et on vérifie que l’intervalle est suffisamment faible par rapport au besoin. Dans le cas contraire, on effectue de nouvelles mesures. Suivant le type de reproductibilité que vous recherchez, il peut exister quelques subtilités de calculs, notamment dans le cas où vous souhaitez extraire la répétabilité des séries de mesure dont vous disposez pour calculer la reproductibilité …

 

Question : Les covariances sont-elles additives?

Réponse : Oui. Les covariances s’additionnent avec les variances pour donner la variance finale du phénomène. Mais attention, les propriétés des écarts-types sont fonction de la loi de probabilité du phénomène en présence. Lorsqu’il y a des covariances entre les phénomènes qui composent le phénomène d’intérêt, ce dernier peut ne pas être gaussien et sa variance globale, calculée en additionnant les variances et les covariances, peut ne pas être une variance de loi normale …

 

Question : Qu’est-ce que le coefficient r², coefficient de corrélation, introduit à la 45^ème minute?

Réponse : Il s’agit du coefficient de corrélation linéaire entre deux variables. Ce sujet n’est pas traité dans ce séminaire, il mériterait un long développement. Pour résumer, on peut néanmoins indiquer qu’il s’agit d’un paramètre qui varie entre 0 et 1 et qui indique la force d’une relation « linéaire » entre deux variables.

Cas r²=0 : indépendance « linéaire » des x et des y donc la courbe f(x)=y n’a pas de sens.

Cas r²=1 : la relation y= f(x) est « parfaite ».

Dans la pratique, et lorsqu’on recherche une relation entre deux variables, on apprécie de trouver un r² proche de 1 même s’il peut exister une relation très forte que ce coefficient ne détecte pas. Il faut donc l’utiliser avec pas mal de recul …

 

Question : Loi uniforme et Loi équiprobable sont-ils des synonymes?

Réponse : Oui, ces deux termes renvoient à la même loi. On l’appelle parfois loi rectangle également, voire même carré parfois !

 

Question : Ecart type = incertitude de mesure ?

Réponse : En aucun cas !!! En fait, l’écart-type ne représente que la dispersion du processus de mesure. Or, l’incertitude associée à une mesure peut également subir un biais, et ceci pour de multiples raisons : instrument, conditions environnementales « moyennes » de la mesure, méthode …

Par ailleurs, pour qu’un écart-type représente la totalité de la dispersion du processus de mesure, il faut qu’il ait été calculé à partir de données pour lesquelles on s’est assuré que tous les facteurs qui amènent de la dispersion aient bien varié. On peut répéter 10 000 fois une mesure avec un opérateur donné, la série de mesures ne contiendra pas la variabilité inter-opérateurs, idem pour les instruments, pour les conditions environnementales … Pour avoir des chances que « tout bouge », on pratique des essais inter-laboratoires mais l’évaluation du biais nécessite alors que les entités soumises à cet essai soient de valeurs connues …

 

Question : Est-ce que « l’addition » de lois uniformes indépendantes donnent toujours une loi normale ?

Réponse : Le théorème central limite démontre que lorsqu’on mélange des lois indépendantes, on converge vers une loi normale. Néanmoins, pour que le mélange de lois de probabilité donne une loi raisonnablement assimilable à une loi normale, il faut respecter 2 conditions. Il ne faut pas que l’une des causes élémentaires ait un poids supérieur à 30% dans le « mélange ». Cela impose donc qu’il y ait au moins 3 lois uniformes de même « force » (comprendre « de même variance ») dans le mélange. Une loi uniforme qui varierait dans un intervalle de ± 100 et qui se mélangerait avec deux autres lois uniformes qui, elles, varieraient dans un intervalle de ± 1 donnerait une loi uniforme qui varierait dans un intervalle d’à peu près ±100. Dans cette hypothèse en effet, la première loi pèse pratiquement 100% de la variance globale, elle est donc la loi résultante, les autres étant négligeables. La seconde condition est que les lois en présence soient indépendantes entre-elles mais elles le sont par hypothèse dans la question !

Pour voir ou revoir ce webinar en replay

 

…et maintenant?

Ce webinar a été le premier proposé par Deltamu. Nous en proposerons d’autres dans les prochaines semaines. Avez-vous des sujets à nous proposer? N’hésitez pas à nous les indiquer par mail.

Les dates et sujets des nouveaux webinars seront annoncés via les réseaux sociaux et notre Newsletter.

Suivez-nous sur les réseaux sociaux et/ou inscrivez-vous à notre Newsletter!