2021
| Mais qu’est-ce que vous voulez faire avec ça ! |  |
Plus le temps passe et plus je trouve notre métier archaïque. J’écrivais récemment que la métrologie avait loupé sa 3ème révolution et je mesure à quel point ce fiasco est puissant lorsque j’anime des formations.
J’interviens avec bonheur dans le Mastère Spécialisé « Data Science pour l’Ingénierie », porté par l’école Sigma Clermont. Il s’agit de former de jeunes ingénieurs aux techniques de la data science. La véracité des données mesurées, ma discipline, est évidemment au cœur de ces nouvelles technologies. Le 4ème V du Big Data, socle de la Data Science, est là pour nous le rappeler …
Seulement voilà, comment expliquer à ces jeunes gens brillants l’espèce de tambouille dans laquelle la pratique « ISO 9000 » de la métrologie nous a tous collectivement plongés ? Je peux comprendre que les praticiens ne soient pas choqués par ce qui suit car ils le vivent, comme moi-même, depuis toujours. Ils pensent donc naturellement que cela est normal. Mais quelques mots d’explications s’appuyant sur des publications officielles devraient tout de même finir par nous réveiller collectivement… Ce réveil, que j’appelle de tous mes vœux, devrait conduire à des modifications profondes des prestations des « étalonneurs » qui ne les ont malheureusement pas beaucoup faites évoluer en 30 ans. Personnellement, je ne vois pas de différences fondamentales avec mes débuts dans le métier, en 1988 …
Point 1 : Les étalonneurs nous doivent les erreurs des instruments mais ils ne voient en réalité que des erreurs de mesure …
J’ai donné, lors du Xème Congrès International de Métrologie qui s’est tenu en 2001 à Saint-Louis (Haut-Rhin), une conférence dont le titre était un peu provocateur : « Et si le VIM s’était trompé ? ». Il s’agissait, à l’époque, de comparer les définitions de « Erreur de mesure » et « Erreur d’indication d’un instrument de mesure ». Objectivement, il était assez facile de mettre le doigt sur le problème et même d’esquisser la réponse : Oui, le VIM se trompe sur ce sujet car « la valeur mesurée » et « la valeur indiquée par l’instrument de mesure » sont les mêmes, et les conséquences ne sont pas neutres …
Si, à l’époque, je n’avais pas été vraiment écouté, deux documents de la littérature officielle de la métrologie française ont finalement reconnu que, pour le coup, je ne me trompais pas ! Le VIM l’a aussi en quelque sorte reconnu en supprimant, dans sa version de 2008, la définition de « Erreur d’indication d’un instrument de mesure » …


Ces deux documents provenant de deux groupes d’experts distincts, on devrait pouvoir en conclure que les étalonneurs professionnels savent depuis longtemps que ce qu’ils mesurent n’est pas exactement ce qu’ils indiquent (à moins qu’ils ne s’instruisent pas auquel cas ce serait plus que grave). Ils évaluent donc, dans leur laboratoire et dans des conditions particulièrement bien maitrisées, des erreurs de mesure (versus des erreurs d’indication) en observant la différence entre la valeur portée par l’instrument et la valeur connue de leur étalon. Cette erreur est bien une erreur de mesure dans laquelle se mélangent les erreurs locales propres à l’instrument mais aussi, et parfois surtout, les erreurs propres au laboratoire lui même ! Pour simplifier, et encore actuellement, ils nous vendent les erreurs qu’ils ont observées (et qu’ils appellent souvent « erreur d’indication », notamment en métrologie dimensionnelle et que d’autres appellent « correction », ce qui est pire, en faisant la soustraction dans l’autre sens) et l’erreur la plus grande qu’ils risquaient d’observer du fait de leur propre responsabilité, c’est à dire leur propre incertitude : l’incertitude d’étalonnage (qu’on pourrait aussi appeler « l’incertitude des étalonneurs »)
Point 2 : Démonstration
Pour étayer cette observation, analysons ensemble des résultats d’étalonnage obtenus par un laboratoire COFRAC sur un micromètre 0-25 mm à affichage numérique au 1/1000 de mm (exemple réel).
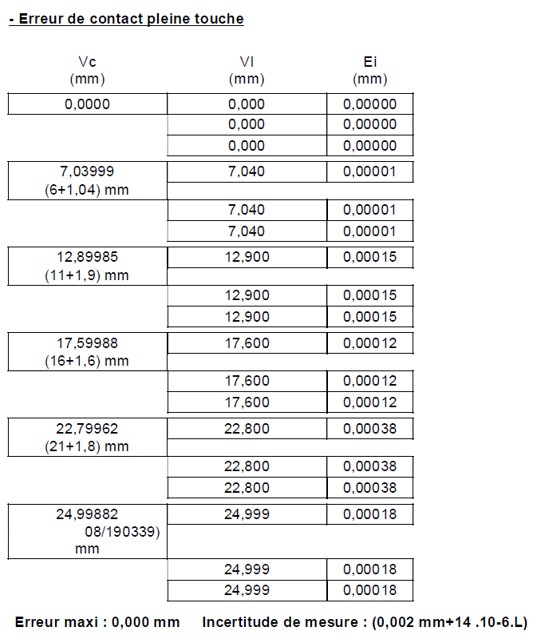
On remarque dans ces résultats que l’erreur « maxi » est égale à 0,00038 mm (si on ne tient pas compte de l’arrondi) avec une incertitude élargie de 0,00235 mm (application de la formule pour L = 25mm). Ainsi donc, dans ce cas, l’incertitude d’étalonnage est plus de 6 fois plus grande que l’erreur « maxi », c’est à dire, plus précisément, l’erreur la plus grande observée sur 6 points seulement, alors que le micromètre dispose de 25 x 1000 = 25 000 possibilités de lecture différentes !!!!
Deux remarques s’imposent à ce stade :
1 : Comment un laboratoire d’étalonnage peut-il encore prétendre avoir vu la plus grande erreur du micromètre en n’observant que 6 points sur 25 000, soit seulement 0,024% des possibilités offertes par le micromètre ?
2 : Pourquoi, alors qu’il ne voit que des écarts si petits devant son incertitude propre, et sachant ce que je viens de rappeler plus haut, ne statue-t-il pas plus simplement sur le fait qu’il n’a rien vu ? Et s’il n’a rien vu dans les conditions d’un laboratoire accrédité, en mesurant des étalons quasi parfaits confortablement installé dans un fauteuil, comment peut-on imaginer que l’instrument va avoir une influence sur la qualité d’une mesure industrielle dont on connait les conditions parfois compliquées ?
Et cette situation n’est pas rare… En effet, dans l’annexe D du FD X 07-039, on peut lire :

Voilà donc les choses clairement dites, et dans une quasi-norme, ce n’est pas rien ! Il y a un problème dans l’évaluation des incertitudes d’étalonnage mais cela ne semble pas émouvoir grand monde, le petit ronron installé depuis 1990 continue tranquillement sans se soucier des besoins réels des utilisateurs, quelle tristesse !
Tout étalonneur sait que si on étalonne un instrument, c’est pour tenter de quantifier ses performances métrologiques pour pouvoir conclure sur deux points. Il le sait parce qu’il fait lui aussi étalonner ses propres instruments/étalons et il calcule lui-aussi des incertitudes (de façon discutable si j’en crois ce qui est écrit au dessus ;-)) :
- Cet instrument nécessite-t-il une correction (Cf la modélisation qui devrait faire partie intégrante d’un étalonnage depuis 2008, soit depuis plus de 12 ans !). Si oui, quelle est la correction à appliquer et son incertitude associée, incertitude qui sera alors intégrée dans le calcul d’incertitude du processus de mesure qui utilise l’instrument. Tous les étalonneurs font cela normalement dans leurs propres calculs …
- Quelle est la part aléatoire restante après correction, cette part aléatoire étant à déterminer, soit autour du modèle (cas des corrections), soit directement autour de « 0 » (pour les erreurs) dans le cas où il n’y a pas de correction ?
Alors que ces calculs sont réalisables automatiquement à partir d’applications gratuites disponibles via le CFM (M-CARE) ou le LNE (REGPOLY) ou qu’ils peuvent parfaitement intégrer les méthodes dans leurs logiciels d’exploitation, les laboratoires continuent à faire comme si de rien n’était en proposant des « vérifications » basées sur des erreurs de mesure (versus des erreurs des instruments de mesure) comme nous l’avons compris plus haut. De plus, ces vérifications sont le plus souvent réalisées par comparaison à des limites proposées par les normes, donc le plus souvent sans aucun rapport avec le besoin propre de chaque utilisateur. La norme ne peut pas satisfaire toutes les configurations d’utilisation, et elle ne le prétend pas tellement c’est évident !
Je connais bien la réponse des étalonneurs : « Les clients ne nous le demandent pas ! » Personnellement, pas plus que le lecteur de cet article, je n’ai rien demandé à Apple mais je suis bien content d’avoir un smartphone. Est-ce aux clients, très majoritairement contraints non pas par un besoin technique mais pour satisfaire une exigence mal comprise de la norme, de demander des solutions ou aux « experts » de les proposer ? Si les « experts » faisaient leur travail de vulgarisation (qui peut le faire sinon ?), nous n’en serions très certainement plus là depuis longtemps … La rente doit être confortable !
Point 3 : Conséquences
Pour ne pas faire le petit effort d’intégrer un peu de calculs dans leurs logiciels, les étalonneurs se contentent donc depuis 30 ans, sur la base de 0,024% des observations possibles (dans ce cas précis, mais pas beaucoup plus dans une grande partie des autres cas), de déclarer des « conformités », sans tenir compte de leurs incertitudes (dans de nombreux cas). En outre, le fait d’indiquer « Conforme » rassure probablement beaucoup de monde mais la question est de savoir conforme à quoi ! Si c’est pour déclarer que le micromètre est conforme à une EMT de +/- 6 µm alors même qu’ils n’ont probablement rien pu percevoir des défauts propres à l’instrument, c’est un peu fort en chocolat, non ?.
Et en restant enfermés dans ce monde dépassé, ils nous obligent quasiment (Cette pratique ayant fini par s’installer dans les esprits) à enseigner que dans ce cas, il faudrait considérer l’EMT en loi uniforme et considérer également leurs incertitudes (un comble !) dans le calcul d’incertitude d’utilisation du micromètre. Cela se traduit par deux lignes dans le bilan d’incertitude (auxquelles il faudra bien sur ajouter toutes les autres vraies causes d’incertitude du processus industriel étudié) :
| Cause d’incertitude | Erreur maxi | Loi | Ecart-type |
| EMT Micromètre | 0,006 | Uniforme | 0,0034641 |
| U étalonnage | 0,00235 | Normal 95% | 0,001175 |
Or, quelques petits calculs élémentaires auraient permis de conclure que l’instrument était tout simplement négligeable dans le processus de mesure (la démonstration suit) et que ces deux erreurs qui seront probablement conséquentes dans l’incertitude finale n’ont en fait pas lieu d’être dans le bilan … Ceci dit, ça a le mérite, pour eux, de rester utile pour continuer à faire croire qu’il faudra réétalonner cet instrument l’an prochain ! A qui profite le « crime » ?
Démonstration :
La première question à se poser, après un étalonnage, est donc de savoir si l’instrument présente, ou non, un effet prévisible, c’est à dire modélisable ce qui permet une correction. Une simple observation graphique nous dit clairement que non dans cet exemple :
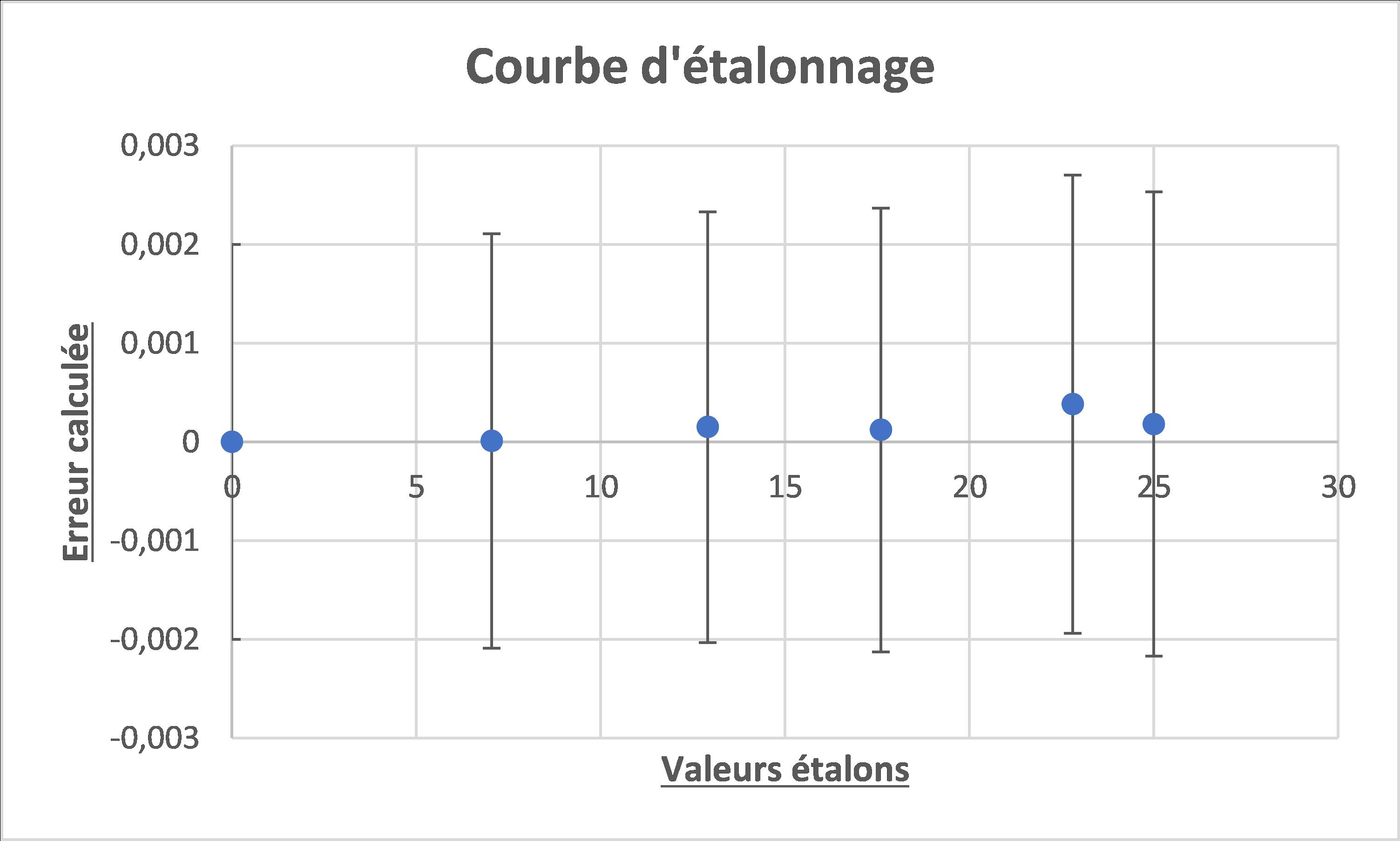
Il y a mille choses à dire sur la modélisation et nous en avons déjà dit beaucoup, notamment au cours de ce webinar. Mais ici, les choses sont très claires : l’instrument ne présente pas de défauts prévisibles, ou en tous cas, les incertitudes d’étalonnage ne permettent pas de les voir. Nous répondons donc aisément à la première question (point a) ci-dessus) que nous devons nous poser pour faire un bilan d’incertitude à l’utilisation de ce micromètre : il n’y a pas besoin de correction, donc pas d’incertitude sur la correction !
Pour ce qui est du point b), un simple calcul d’écart-type sur les erreurs mesurées au cours de l’étalonnage donne le résultat ci-dessous :
| Erreur mesurée | |
| 0 | |
| 0 | |
| 0 | |
| 0,00001 | |
| 0,00001 | |
| 0,00001 | |
| 0,00015 | |
| 0,00015 | |
| 0,00015 | |
| 0,00012 | |
| 0,00012 | |
| 0,00012 | |
| 0,00038 | |
| 0,00038 | |
| 0,00038 | |
| 0,00018 | |
| 0,00018 | |
| 0,00018 | |
| Ecart-type | 0,00013 |
| Incertitude-type d’étalonnage | 0,001 |
| Ratio en variance | 1,70% |
Là encore, on observe que le laboratoire n’a rien vu. L’écart-type des erreurs qu’il a observées ne pèse que 1,7% de l’incertitude type d’étalonnage, ce qui tend à montrer qu’elle n’est pas, une fois encore, évaluée convenablement…
PS : Il faut remarquer ici que l’écart-type des écarts n’est en réalité dû qu’aux écarts des étalons à leur valeur nominale. Il est d’ailleurs stupéfiant de constater que le COFRAC impose de donner les V.C.V (Valeur conventionnellement vraie) des étalons au 1/100 de µm alors que l’instrument a dans ce cas une résolution de 1 µm. Si on regardait uniquement les valeurs mesurées, l’écart-type serait égal à 0 et il conviendrait alors de considérer, par une méthode de type B, l’erreur due à la résolution du micromètre comme seule erreur provenant de lui dans une incertitude. On aurait alors soit 1/(2x√3) ou 1/√3 suivant que nous considérions l’erreur maximale due à la résolution égale à la demi-résolution ou la résolution entière. Ceci ne changerait rien à la conclusion : les erreurs propres au micromètre n’ont pas été vues dans un contexte d’étalonnage, elles sont donc totalement négligeables dans un contexte industriel de mesure !
Point 4 : Conclusion
Tout ça pour ça !
Mon instrument est quasi indétectable dans un laboratoire COFRAC mais il faudrait que je considère, dans mes propres calculs d’incertitude d’utilisation, des erreurs non négligeables qui ne viennent même pas de lui mais du prestataire d’étalonnage. Et ce dernier ne semble pas savoir, ou ne pas vouloir, faire deux calculs simples pour me donner des conclusions pertinentes.
Si cet état de fait peut perdurer tranquillement dans l’univers de l’ISO 9001 (et on s’étonne que la métrologie ne soit pas reconnue !), il n’est pas tolérable que cela continue dans l’industrie 4.0 dont les nouvelles technologies imposent des données fiables. Chez Deltamu, nous prônons la fiabilité des données depuis notre création, il y a plus de 20 ans. Le Big Data et l’Intelligence Artificielle nous donnent raison. J’espère que nous ne devrons pas attendre 20 ans de plus avant d’être entendus. Le risque est grand en effet que nous devions nous passer d’une technologie puissante à cause de pratiques plus que critiquables ! Amis métrologues, la balle est dans votre camp. C’est à nous de jouer pour faire changer les choses, on ne peut pas compter, je le crains, sur les acteurs historiques …


