Il Bayesian Measurement Refinement (B.M.R) viene eseguito in 3 fasi.

Fase 1 : Incertezza di misura

Questo passaggio dovrebbe essere un classico per i metrologi ma richiede, nel caso del B.M.R., una cura molto particolare. Questo per valutare l’incertezza di misura del processo che ha prodotto i dati da affinare. Queste misure esistono, sono state prodotte in un contesto e secondo una metodologia che è necessario analizzare. Questa analisi permette di definire i fattori che intervengono durante le misurazioni, di stimare la rispettiva legge di probabilità (cioè la probabilità che producano un determinato errore durante una misurazione), di valutare eventuali covarianze che possono esistere fra di loro, per coppia,oltre a regolare la legge di distribuzione dell’insieme di leggi di probabilità presenti (incertezza di misura globale).

Nella G.U.M, si considera che la legge di distribuzione degli errori di misura sia una distribuzione normale, basata sul fatto che molti fattori si mescolano. Se questo è effettivamente il caso, li teorema centrale del limite dimostra che la legge risultante da questa mescolanza è effettivamente  una gaussiana. Tuttavia, affinchè ciò sia vero, devono essere rispettate alcune condizioni: indipendenza degli errori che la compongono, nessun fattore con un peso superiore al 30% della variazione globale e almeno 3 fattori nell’incertezza globale.

Occorre sottolineare, ma questo non è lo scopo di questo articolo, che queste condizioni non sono sempre soddisfatte. In effetti, è frequente che una causa possa risultare largamente maggioritaria nell’incertezza. Inoltre, capita molte volte, durante questo calcolo “G.U.M.”, che tutte le cause d’incertezza siano considerate come appartenenti al mondo probabilistico (il che rende possibile usare le proprietà di additività delle medie e delle varianze), cosa alquanto discutibile (Vedi G.U.M.: There may be a pitfall).

Tuttavia, nel caso del B.M.R., non è possibile valutare “ad occhio e croce” l’incertezza di misura. È importante che l’analisi effettuata sia rappresentativa della realtà perchè le misure di cui si dispone, sono molto reali e sono queste che verranno affinate grazie alla conoscenza dell’incertezza. Non si tratta qui di esprimere una dichiarazione di conformità prendendo un rischio minimo, anche se ciò signifca aumentare le incertezze.

La G.U.M S1 permette di approfondire la conoscenza degli errori di misura. Utilizzando la simulazione numerica e facendo variare ogni fattore dell’incertezza globale nella sua area di variazione, è possibile ottenere la legge di probabilità degli errori di misura. In questo contesto, è anche possibile tener conto di qualsiasi covarianza eventualmente esistente generando variabili correlate.

Il metrologo dispone dunque di tutti gli strumenti necessari per una una valutazione obiettiva della realtà delle incertezze di misura, anche se le pratiche odierne dovranno probabilmente essere migliorate, in quanto spesso si limitano ad aumentare l’incertezza, il ché non è lo scopo della B.M.R.

Per esemplificare questo articolo, consideriamo che le incertezze associate ad una serie di misure che dobbiamo affinare rispondano alla seguente valutazione. Dato che tutti i componenti sono gaussiani e sono indipendenti, l’incertezza finale è una distribuzione normale con media -0,2 e scarto tipo 0,109.

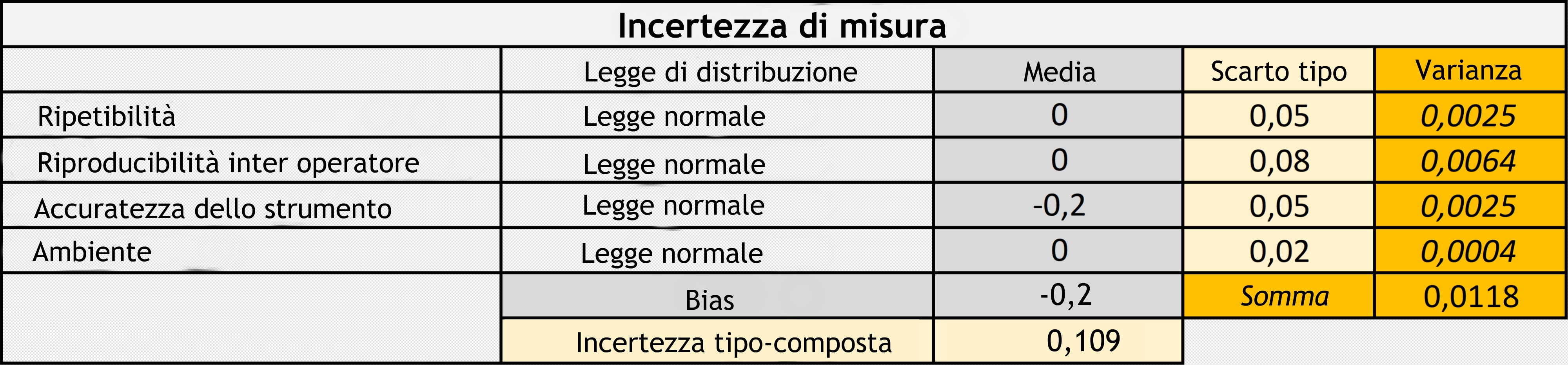
Tabella delle componenti dell’incertezza di misura

Fase 2 : Deconvoluzione

Tutti sanno che una misura risponde all’equazione base della metrologia :

Vale misurato = Valore vero + Errore di misura

Di conseguenza, la distribuzione dei valori misurati è il risltato della miscela della distribuzione dei valori reali sottostanti (che chiameremo legge ” a priori”) e della distribuzione degli errori di misura che si sono prodotti durante le misurazioni (l’incertezza di misura). Possiamo quindi rappresentare il tutto nel modo seguente:

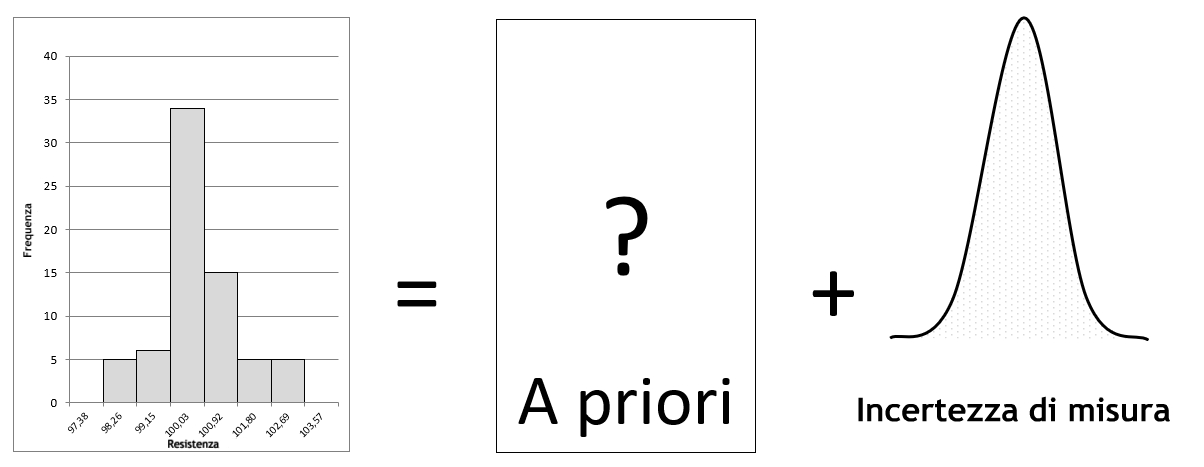
Pertanto, è possibile effettuare anche l’operazione inversa, la deconvoluzione, che consiste nel risolvere l’equazione :

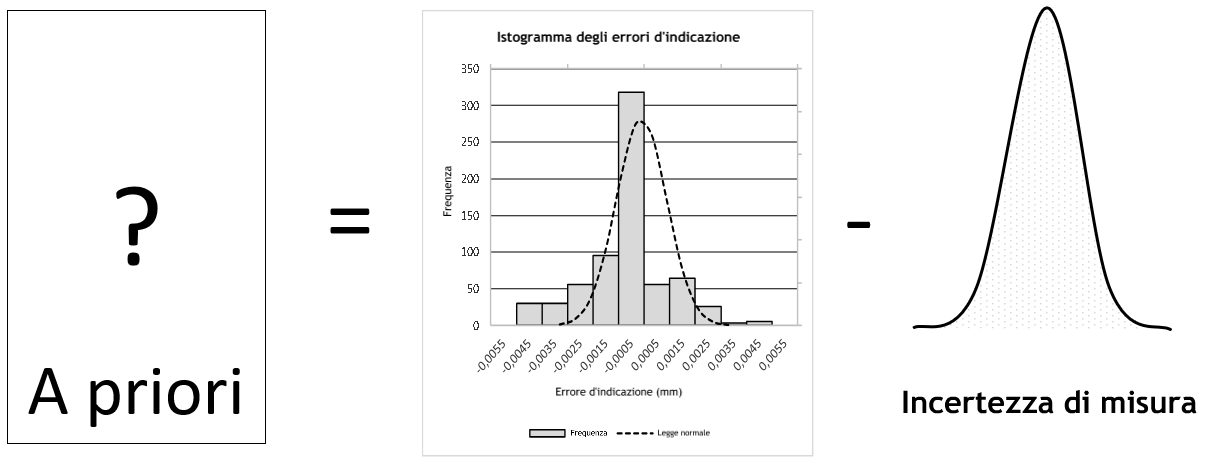
Comprendiamo tutti quindi l’importanza di conoscere la distribuzione degli errori di misura in modo obiettivo. Questa « condicio sine qua non » garantisce la qualità dell’informazione risultante dalla deconvoluzione, cioè l’obiettività della conoscenza a priori della realtà.

La deconvoluzione è molto semplice quando abbiamo a che fare con fenomeni gaussaini, sia per la realtà che per gli errori di misura. In questo caso, sappiamo che la curva di distribuzione dell’a priori è gaussiana, che la sua media è uguale alla media dei valori misurati meno la distorsione dovuta all’incertezza di misura (essa stessa risultato della somma delle distorsioni di tutti i fattori componenti) e che la varianza è uguale alla varianza dei valori misurati meno la varianza dell’incertezza di misura. Quando le leggi non sono gaussiane, la deconvoluzione diventa molto più complicata e avremo l’occasione di tonare alle tecniche da applicare in una prossima pubblicazione.

La simulazione numerica è uno strumento interessante per osservare le proprietà che abbiamo appena menzionato. Nella vita di tutti i giorni, non conosciamo mai rigorosamente la realtà, ne le incertezze di misura. Tuttavia, grazie alla simulazione, possiamo fare delle ipotesi e osservarne gli effetti. Immaginando una realtà gaussiana, con media 2,501 e scarto tipo 0,087, è possibile simulare una serie di dati misurati impotizzando un’incertezza di misura composta come presentato nel grafico precedente. Dai dati simulati sulla base delle ipotesi indicate, è possibile, sullo stesso grafico, osservare la distribuzione della realtà e la distribuzione delle misure, poichè le si ottengono tenuto conto dell’incertezza di misura.

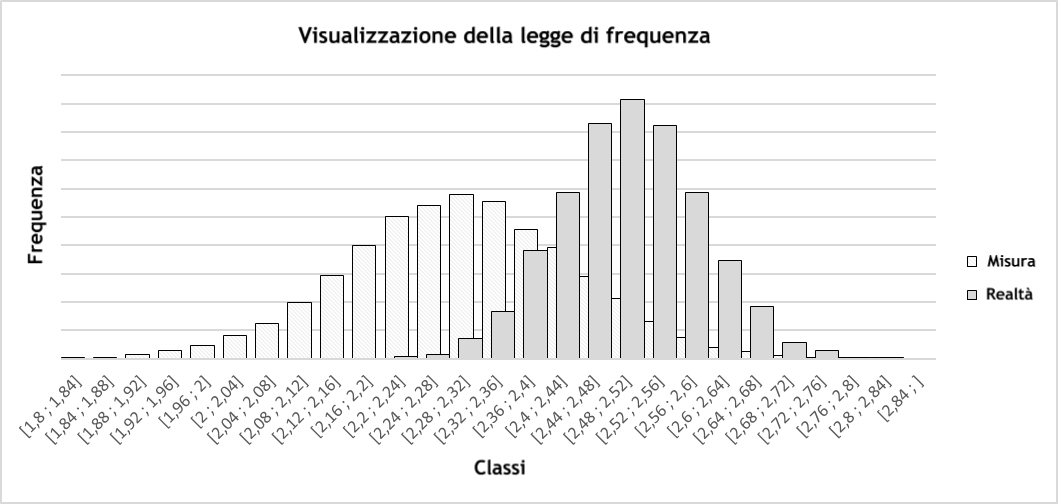
Considerando queste ipotesi, si può vedere quanto possono essere differenti “quello che vediamo” (le misure) e la realtà…lo si vede meglio perchè abbiamo considerato un bias “non corretto” sulla incertezza di misura, ma molte altre situazioni possono essere previste nella realtà (distorsione, nessuna distorsione, dispersione forte, dispersione debole,…). Solo una valutazione obiettiva e realista dell’incertezza di misura permette di comprendere la differenza tra realtà e misure, e la realizzazione di questa valutazione è parte integrante dei compiti del metrologo del 21esimo secolo.

Fase 3 : Perfezionamento dei dati misurati (Inferenza bayesiana)

Thomas Bayes è stato un matematico e pastore britannico della Chiesa presbiteriana, conosciuto per aver formulato il teorema di Bayes, che nella sua formulazione più semplice può essere scritto come segue:

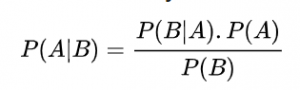
Se chiamiamo A il valore vero e B il valore misurato, questo teorema recita come segue : “La probabilità del valore vero noto il valore misurato è uguale alla probabilità del valore misurato noto il valore vero moltiplicato per la probabilità del valore vero, diviso la probabilità del valore misurato“. In altre parole: il valore vero più probabile che si cela dietro il valore misurato puo’ essere calcolato a partire dalle seguenti informazioni:

• la probabilità di ogni possibile valore vero
• la probabilità di ogni possibile errore di misura

Ogni valore misurato deriva da una moltitudine di possibili combinazioni “valore vero, errore di misura”. Effettivamente, una misura uguale a 2,3 può provenire da diverse combinazioni: …; 2+0,3; 2,01+0,29; 2,02+0,28; …; 2,49-0,19; …

Conoscendo la probabilità di ogni possibile valore vero (legge di probabilità a priori determinata nella fase 2 qui sopra) e la probabilità ogni possibile errore misurato (incertezza di misura determinata nella fase 1 qui sopra), è possibile calcolare la probabilità di ogni combinazione all’origine della misura, quindi la combinazione più probabile, e di conseguenza determinare “il valore vero più probabile che si nasconde” dietro il valore misurato.

Nel caso di una gaussiana, possiamo dimostrare che questo valore più probabile, indicato con µ_{A posteriori}, nota la leggi a priori, l’incertezza di misura e il valore misurato, è uguale a:

µ_{A posteriori} = (1 – θ) x µ₀ +θ x (η_{m – Distorsione di misura)} 

Con: θ = 1 / (1 + µ²/µ₀²⁾

Dove µ₀ rappresenta la media della legge a priori, η_m il valore misurato, “Distorsione di misura” la media della legge “Incertezza di misura”, u² la varianza della legge “incertezza di misura” e u₀² la varianza della legge “a priori”.

Questa semplice relazione matematica (in un “contesto gaussiano”) permette di realizzare una elaborazione ulteriore di ogni valore misurato con l’obiettivo d’affinarli, cioè renderli più rappresentativi della realtà. Possiamo quindi osservare il risultato di questo affinamento, osservando sullo stesso grafico, la realtà (che non conosceremo mai rigorosamente), le misure disponibili e le misure affinate (sapendo tutto ciò che sappiamo su come ottenere le misure ). Vi lascio giudicare:

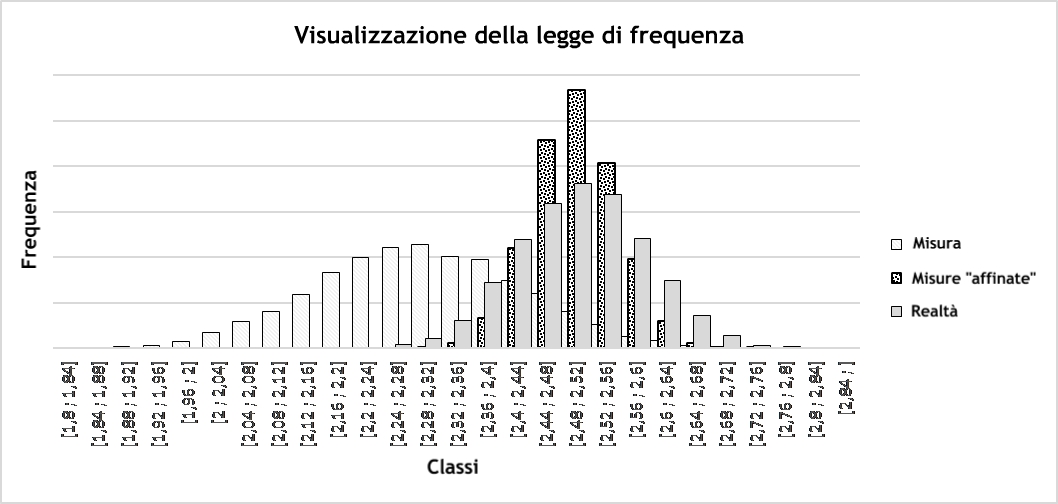
Conclusioni

Anche se le “misure affinate” non sono esattamente uguali alla legge a priori (realtà), possiamo tutti convenire che sono qualitativamente migliori rispetto ai dati misurati “grezzi”. Questa operazione d’affinamento esige il rispetto di diverse condizioni. Ovviamente, il processo di cui stiamo provando a determinare la legge a priori deve essere stabile. In effetti ogni deriva nel tempo, in tendenza o in dispersione, induce un cambiamento della leggi a priori e quindi invalida tutti i calcoli post-eleborazione È quindi essenziale capire cosa stiamo facendo, per assicurarsi che la legge a priori , come è noto, sia ancora attuale e che le incertezze di misurazione siano sempre realistiche (cioè coerenti con la loro realtà). Effettivamente anche queste possono deviare a causa di un fattore (ad esempio lo strumento) o di un altro (ad esempio le condizioni dell’ambiente). La pratica del Bayesian Measurement Refinement richiede quindi delle buone capacità di elaborazione dei dati. I metrologi o i data scientist devono acquisirle e Deltamu può aiutarli. Siamo disponibili anche a darvi una mano per applicare questo trattamento sui vostri dati…