2020
| Bayesian Measurement Refinement – Exemple d’application |  |
Le Bayesian Measurement Refinement (B.M.R) se conduit en 3 étapes.
Phase 1 : L’incertitude de mesure
Cette étape devrait être classique pour les métrologues mais elle nécessite, dans le cadre du B.R.M, un soin tout particulier. Il s’agit d’évaluer l’incertitude de mesure du processus qui a produit les données à raffiner. Ces mesures existent, elles ont été produites dans un contexte et suivant une méthodologie qu’il faut analyser. Cette analyse permet de dresser la liste des facteurs qui interviennent lors des mesures, d’estimer leur loi de probabilités respective (c’est à dire la probabilité qu’ils produisent telle ou telle erreur lors d’une mesure), d’évaluer les éventuelles covariances qui peuvent exister entre eux, par paires, puis de statuer sur la loi de distribution du mélange des lois de probabilité en présence (incertitude de mesure globale).
Dans le G.U.M, il est considéré que la loi de distribution des erreurs de mesure est une loi Normale, en s’appuyant sur le fait que de nombreux facteurs se mélangent. Si tel est effectivement le cas, le théorème central limite démontre que la loi résultant de ce mélange est effectivement gaussienne. Pour que ce soit vrai, il faut néanmoins que certaines conditions soient respectées : indépendance des erreurs qui la composent, pas de facteur pesant plus de 30% de la variation globale et au moins 3 facteurs dans l’incertitude globale.
Il faut ici souligner, mais ce n’est pas l’objet de cet article, que ces conditions ne sont pas toujours respectées. En effet, il est fréquent qu’une cause puisse être largement majoritaire dans l’incertitude. Il est aussi fréquent, dans ce calcul « G.U.M », que toutes les causes d’incertitude soient considérées comme appartenant au monde probabiliste (ce qui permet d’utiliser les propriétés d’additivité des moyennes et des variances) alors que ce principe est très discutable (Lire G.U.M : il y a peut-être un hic …).
Or, dans le cas du B.M.R, il n’est pas envisageable d’évaluer « à la louche » l’incertitude de mesure. Il est important que l’analyse que nous faisons soit représentative de la réalité car les mesures dont nous disposons, elles, sont bien réelles et ce sont elles qui vont être raffinées grâce à la connaissance de l’incertitude. Il ne s’agit pas ici de donner un avis de conformité en prenant un minimum de risque, quitte à majorer pour cela les incertitudes.
Le G.U.M S1 permet, quant à lui, d’aller plus loin dans la connaissance des erreurs de mesure. En utilisant la simulation numérique et en faisant varier chaque facteur de l’incertitude globale dans sa zone de variation, il est possible d’obtenir la loi de probabilité des erreurs de mesure. Dans ce cadre, il est également possible de tenir compte des covariances éventuelles existantes en générant des variables corrélées.
Le métrologue dispose donc des outils nécessaires à une évaluation objective de la réalité des incertitudes de mesure, même si les pratiques actuelles devront probablement être améliorées du fait qu’elles se contentent souvent de majorer l’incertitude, ce qui n’est pas l’objectif dans le B.M.R.
Afin d’illustrer cet article, nous considérerons que les incertitudes associées à une série de mesure que nous devons raffiner répondent au bilan suivant. Puisque toutes les composantes sont gaussiennes et indépendantes, l’incertitude finale est une loi normale de moyenne -0,2 et d’écart-type 0,109.

Bilan des composantes de l’incertitude de mesure
Phase 2 : La déconvolution
Chacun sait qu’une mesure répond à l’équation de base de la métrologie :
Valeur mesurée = Valeur vraie + Erreur de mesure
En conséquence, la distribution de valeurs mesurées est le fruit du mélange de la distribution des valeurs vraies sous-jacentes (que nous appellerons loi « a priori ») et de la distribution des erreurs de mesure qui se sont produites au cours des mesures (l’incertitude de mesure). On peut donc représenter les choses de la façon suivante :
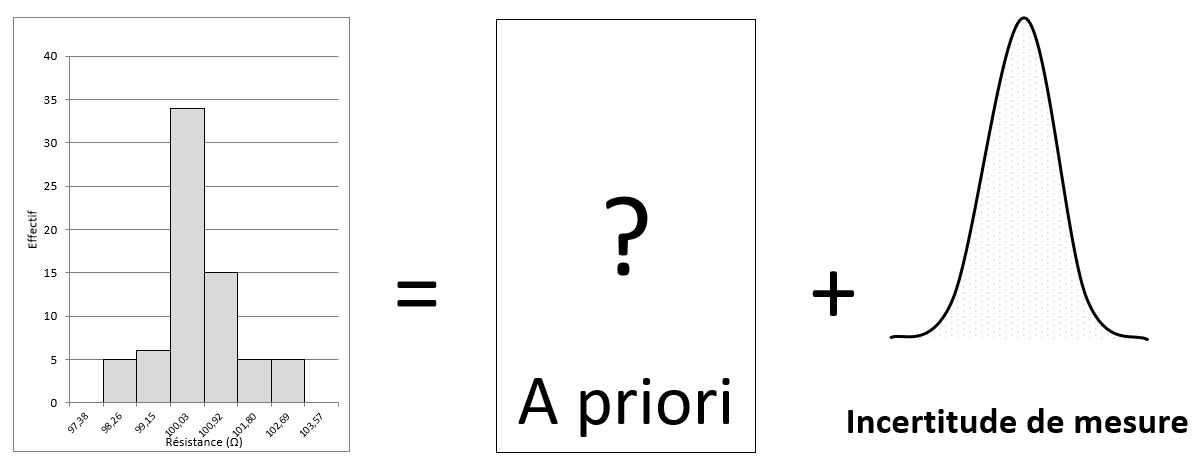
Dès lors, il est possible de réaliser l’opération inverse, la déconvolution, qui consiste à résoudre l’équation :
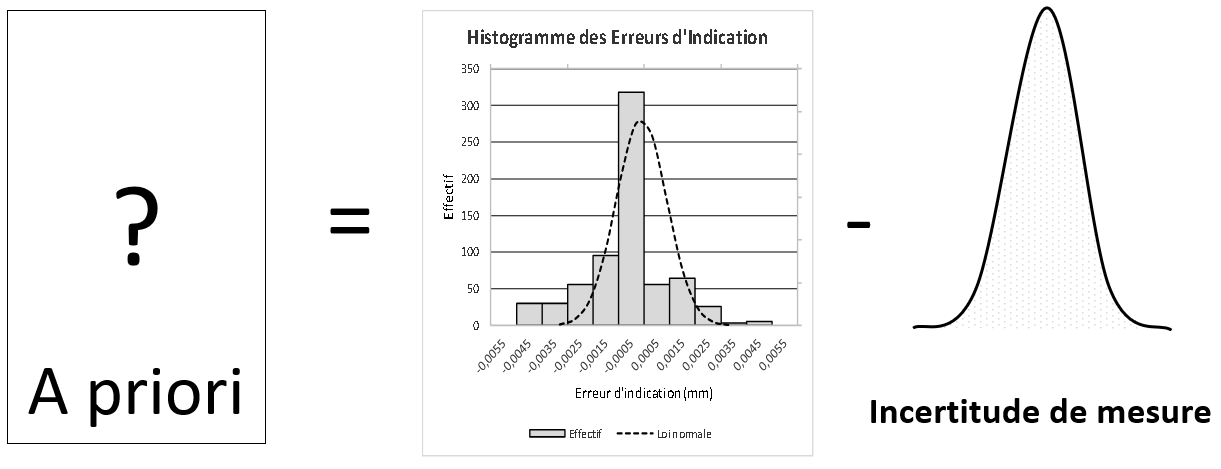
Chacun comprend ici l’importance de connaitre la distribution des erreurs de mesure de façon objective. Cette condition, sine qua non, garantit la qualité de l’information résultant de la déconvolution, c’est à dire l’objectivité de la connaissance a priori de la réalité.
Cette déconvolution est d’une simplicité enfantine lorsque nous avons à faire à des phénomènes gaussiens, pour la réalité et pour les erreurs de mesure. Dans ce cas, on sait que la loi de distribution de l’a priori est gaussienne, que sa moyenne est égale à la moyenne des valeurs mesurées moins le biais de l’incertitude de mesure (lui-même égal à la somme des biais des facteurs qui la composent) et que sa variance est égale à la variance des valeurs mesurées moins la variance de l’incertitude de mesure. Lorsque les lois ne sont pas gaussiennes, la déconvolution devient plus compliquée et nous aurons l’occasion de revenir sur les techniques à mettre en oeuvre dans le cadre d’autres publications.
La simulation numérique est un outil intéressant pour observer les propriétés que nous venons d’évoquer. Dans la vraie vie, on ne connait jamais strictement la réalité, ni les incertitudes de mesure. Par simulation en revanche, on peut se donner des hypothèses et observer leurs effets. En imaginant une réalité gaussienne, de moyenne 2,501 et d’écart-type 0,087, il est possible de simuler une série de données mesurées sous hypothèse d’une incertitude de mesure composée telle que présentée dans le tableau précédent. A partir des données simulées sur la base des hypothèses annoncées, il est possible, sur un même graphique, d’observer la distribution de la réalité et la distribution des mesures, telles que nous les obtenons du fait de l’incertitude de mesure.
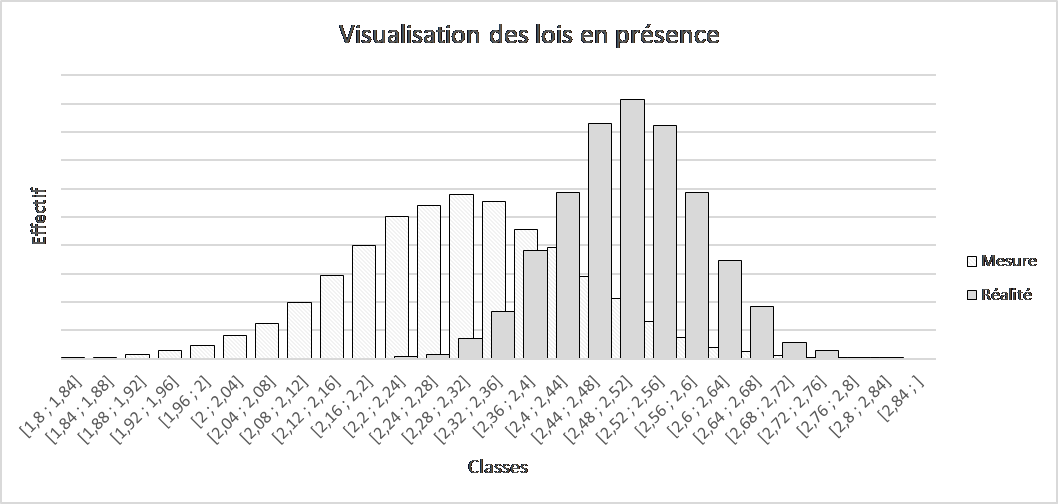
Sous de telles hypothèses, on voit à quel point « ce que nous voyons » (les mesures) et la réalité peuvent être différents … On le voit d’autant mieux que nous avons envisagé un biais « non corrigé » sur l’incertitude de mesure mais de nombreuses autres situations sont envisageables dans la réalité (biais, pas de biais, dispersion importante, dispersion faible, …). Seule une évaluation objective et réaliste de l’incertitude de mesure permet de savoir ce qu’il en est de cette différence entre réalité et mesures, et cela relève de la fonction du métrologue du XXIème siècle.

Phase 3 : Le raffinage des données mesurées (Inférence bayésienne)
Thomas Bayes est un mathématicien britannique et pasteur de l’Église presbytérienne. Il est connu pour avoir formulé le théorème de Bayes qui peut s’écrire, dans sa formulation la plus simple :
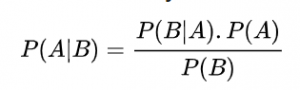
Si on appelle A la valeur vraie et B la valeur mesurée, ce théorème se lit de la façon suivante :« La probabilité de la valeur vraie sachant la valeur mesurée est égale à la probabilité de la valeur mesurée sachant la valeur vraie multipliée par la probabilité de la valeur vraie divisée par la probabilité de la valeur mesurée ». Autrement dit, la valeur vraie la plus probable qui « se cache » derrière la valeur mesurée peut se calculer à partir des informations que sont :
- la probabilité de chaque valeur vraie possible
- la probabilité de chaque erreur de mesure possible
Chaque valeur mesurée résulte d’une multitude de combinaisons possibles « Valeur vraie, erreur de mesure ». En effet, une mesure égale à 2,3 peut provenir de plusieurs combinaisons : …; 2+0,3; 2,01+0,29; 2,02+0,28; …; 2,49-0,19; …
En connaissant la probabilité de chaque valeur vraie possible (Loi de probabilité « a priori » déterminée en phase 2 ci-dessus) et la probabilité de chaque erreur mesurée possible (Incertitude de mesure déterminée en Phase 1 ci-dessus), il est possible de calculer la probabilité de chacune des combinaisons à l’origine de la mesure, donc la combinaison la plus probable et par suite déterminer « la valeur vraie la plus probable qui se cache » derrière la valeur mesurée.
Dans le cadre gaussien, on peut démontrer que cette valeur la plus probable, notée µA posteriori sachant la loi a priori, l’incertitude de mesure et la valeur mesurée, est égale à :
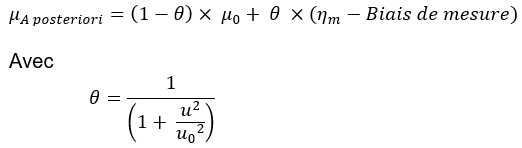
Où µ0 représente la moyenne de la loi a priori, ηm la valeur mesurée, « Biais de mesure » la moyenne de la loi « Incertitude de mesure », u2 la variance de la loi « incertitude de mesure » et u02 la variance de la loi a priori.
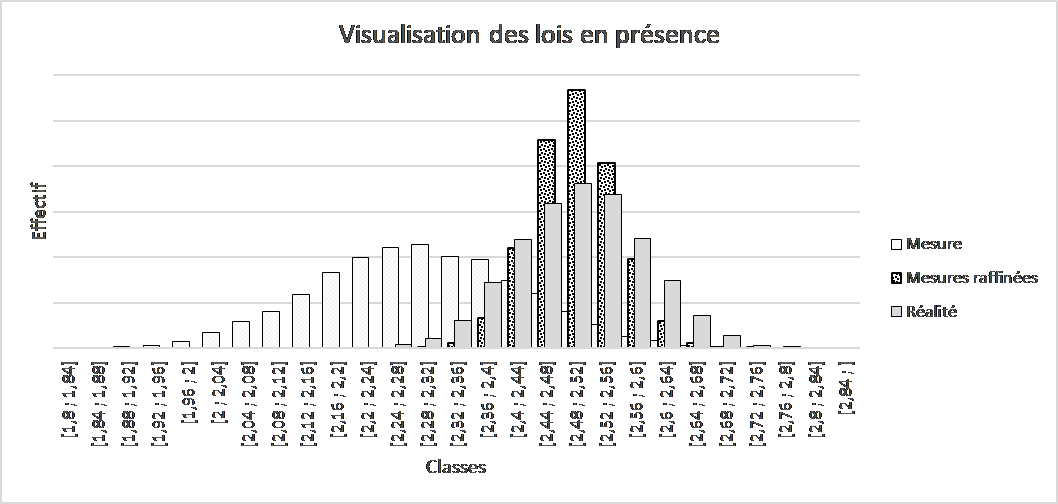
Cette relation mathématique simple (dans le monde gaussien) permet de réaliser un post traitement de chaque valeur mesurée dans l’objectif de les raffiner, c’est à dire les rendre plus représentatives de la réalité. On peut alors observer le résultat de ce raffinage en observant, sur un même graphique, la réalité (que nous ne connaîtrons jamais strictement), les mesures disponibles et les mesures raffinées (sachant tout ce que nous savons sur la façon d’obtenir les mesures). Ce graphique est édifiant, je vous en laisse juges !
Conclusion
Même si les « mesures raffinées » ne sont pas rigoureusement égales à la loi a priori (réalité), chacun pourra convenir qu’elles sont de bien meilleure qualité que les données mesurées brutes. Cette opération de raffinage exige de nombreuses conditions. Il faut évidement que le procédé dont on cherche à déterminer la loi a priori soit stable. En effet, toute dérive dans le temps, en tendance ou en dispersion, induit un changement de la loi a priori et invalide ainsi tous les calculs du post traitement. Il est donc indispensable de comprendre ce que l’on fait, de s’assurer que la loi a priori, telle qu’elle est connue, est toujours d’actualité et que les incertitudes de mesure sont toujours réalistes (c’est à dire conformes à leur réalité). Elles aussi peuvent dériver, à cause d’un facteur (par exemple l’instrument) ou un autre (par exemple les conditions environnementales). La pratique du Bayesian Measurement Refinement impose donc de réelles capacités à traiter des données. Les métrologues ou les data scientists doivent les acquérir et Deltamu peut vous y aider.Nous pouvons aussi vous aider à mettre en place ce traitement sur vos données …


